[자료구조와 알고리즘 | 파이썬] Dynamic Programming(동적계획법) - 다이나믹 프로그래밍; DP
2022.12.31- -
자료구조와 알고리즘(with Python) 카테고리에서는 해당 알고리즘 및 자료구조로 코딩 문제를 잘 풀기 위해 파이썬 언어로 중요한 점들을 위주로 기술한 글입니다.
만약 DP에 대한 더 심화적이고 구체적인(이론) 내용을 보고 싶으신 분들은 아래 링크를 참고해주세요.
[CS 지식/자료구조와 알고리즘(Java)] - [Algorithm] Dynamic Programming(다이나믹 프로그래밍) 알고리즘
[Algorithm] Dynamic Programming(다이나믹 프로그래밍) 알고리즘
이번 시간에는 다이나믹 프로그래밍(동적 계획법 ,DP)에 대해서 배워 보도록 하겠습니다. 1. 다이나믹 프로그래밍이란? Dynamic Programming 줄여서 DP(또는 동적 계획법)는 특정 범위까지의 값을 구하
cdragon.tistory.com
1. Dynamic Programming (동적 계획법)
greedy algorithm(그리디 알고리즘)과 더불어 dynamic programming(다이나믹 프로그래밍)은 코딩 문제에서 굉장히 많이 쓰이는 알고리즘입니다.
1-1. Fibonacci series (피보나치 수열)
다이나믹 프로그래밍이 어떻게 동작하는지 이해하기 위해 다음 예제에 대해 생각해 봅시다. 아래 이미지는 숫자가 나열된 피보나치 수열을 나타내고 있습니다.

피보나치 수열은 아래와 같은 수식으로 정의되어 있습니다.

F0과 F1은 보통 '피보나치 수'라고 미리 알려져 있는 값입니다.
즉, 피보나치 수열에서 0번째값와 1번째값은 각각 0과 1로 항상 정해져 있습니다.
1-2. Recursive implementation (재귀 구현)
import time
start_time = time.time()
def fibonacci(n):
if n < 2:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
print(fibonacci(36))
print(time.time() - start_time)14930352 8.691221952438354

피보나치 수열 계산을 재귀 알고리즘을 통해 계산을 하게 되면 똑같은 계산 과정이 (중복) 반복이 되면서 일어나게 됩니다.
위 그림은 n이 7일 때의 fibonacci 결과를 tree로 나타낸 것인데, 위 코드에 나온 것처럼 n=36에 대한 fibonacci 결과를 tree로 구현한다면 규모가 너무 커서 그 안의 중복 역시 수 없이 많은 구조를 갖게 되어 실행 결과가 8초가 나오는 것처럼 확실히 좋지 않은 성능을 야기하게 된다는 것을 알 수 있습니다.
1-3. Dynamic Programming (다이나믹 프로그래밍)이란?
그래서 우리는 이 중복된 알고리즘을 더욱 효율적으로 바꿔야 합니다.
동적 계획법이라고도 하는 다이나믹 프로그래밍은 divide-and-conquer(분할 정복)처럼 문제를 풀긴 하는데 하위 문제들에 대한 솔루션들을 결합해 가면서 문제를 풀어나가는 알고리즘을 말합니다.
여기서 말하는 프로그래밍이란 컴퓨터 코드를 써내려갈 때의 프로그래밍이 아닌 tabular method 자체를 지칭합니다.
- tabular method: 테이블에 기록하는 방식
분할 정복 알고리즘은 문제를 분리된 여러 하위 문제들로 나누고, 그 하위 문제를 재귀적으로 해결한 다음 각각의 해결책을 결합하여 원래 문제(original problme)를 해결하는 식입니다.
이와 대조적으로 다이나믹 프로그래밍은 그 하위문제라는 것들이 overlap(겹치다)될 때 적용할 수 있습니다.
- 즉, 하위 문제들이 하위-하위 문제를 공유할 때
이러한 맥락에서 분할정복 알고리즘은 필요 이상의 작업을 수행함으로써 공통된 하위 문제를 반복적으로 해결하게 됩니다.
이와 대조적으로 다이나믹 프로그래밍 알고리즘은 각 하위 문제를 딱 한번만 해결한 후에 그 답을 표(table)에 저장하므로 각 하위 문제를 해결할 때마다 답을 다시 계산하는 작업을 피할 수 있는 것입니다.
- 나중에 또 중복되어 나왔을 때 사용하기 위해서 작은 size의 문제를 딱 한 번만 풀고 그 푼 결과를 table에 저장해 두는 것.
하노이의 탑(tower of hanoi) 문제의 경우 분할 정복 알고리즘으로 풀 수 있었습니다. 그러나 그 문제에서 나눠졌던 sub-problem들에 대해 중복된 문제는 단 하나도 없었습니다. (해당 내용은 여기를 참조)
즉, 주어진 문제를 subproblem으로 나누었을 때 중복이 없다면 divide-and-conquer,
중복이 굉장히 많이 나온다면 dynamic programming 으로 전략을 생각할 수 있는 것입니다.
다이나믹 프로그래밍은 그래서 계산 시간을 절약하기 위해 추가적인 메모리를 사용하는 것이라고 보시면 됩니다.
이는 시간과 메모리 사이의 trade-off를 생각해야 한다는 의미인데, 계산 시간의 절약은 꽤 큰 영향을 가져옵니다:
- 가령 exponential-time solution(지수-시간 해)이 polynomial-time solution(다항-시간 해)로도 변환될 수 있습니다.
동적 프로그래밍 접근법을 구현하는 데는 보통 두 가지의 동등한(eqaul) 방법이 있습니다.
1-4. top-down with memoization
이 방식은 굉장히 자연스러운 방식으로 절차를 재귀적으로 작성하지만, 결과를 각 하위 문제(일반적으로 배열 또는 해시 테이블)에 저장하도록 수정됩니다.
이 절차는 가장 먼저 이 하위 문제를 이전에 해결했었는지를 체크합니다. 만약 해결된 적이 있는 문제라면 저장된 그 값을 반환하여 현재 레벨에서 추가 계산을 저장하고, 그렇지 않으면 일반적인 방식으로 값을 계산합니다.
그렇기 때문에 가장 최초의 호출이 우리가 구해야 하는 값에 대한 인자로 호출이 이루어지고 재귀를 통해 아래로 내려가면서(top-down) 문제를 해결해 나가게 됩니다.
우리는 여기서 재귀적 절차가 메모되었다고 말합니다.
- 쉽게 말해 이전에 계산한 결과를 기억(remember)하는 것
그리하여 한 size씩 문제를 줄여나갑니다. (by recursion)
- f(n) - > f(n-1) -> f(n-2) -> ...
top-down with memoization 코드
def fibonacci_td(n):
if n < 2:
return n
if _memo[n] is None: # 존재하지 않으면 memo!
_memo[n] = fibonacci_td(n - 1) + fibonacci_td(n - 2)
return _memo[n]
_memo = [None] * 50
print(fibonacci_td(36))
# 14930352
# 0.0 걸린 시간을 측정하면 0.0초임피보나치 수열의 숫자는 기하급수적으로 증가하기 때문에 이를 담기 위한 배열의 크기가 작습니다. 예를 들어 F46 = 1,836,311,903 은 32bit 정수로 나타낼 수 있는 가장 큰 피보나치 수입니다.
- 32-bit integer로 저장할 수 있는 최대 fibonacci 수는 46입니다. (21억 이전까지 저장 가능하기 때문)
- 그 이상은 long long 데이터 타입을 사용해야 합니다.(파이썬은 상관 없음)
알고리즘 동작은 다음과 같습니다.
- 가장 먼저 메모 list에 이미 저장되어 있던 값인지를 확인한다.
- 만약 저장되어 있지 않다면: 더 작은 size의 문제인 subproblem을 나눠서 계산된 결과를 memo에 저장하고
- 만약 저장되어 있다면 해당 인덱스의 memo값을 반환한다.
- 이러면 볼필요한 재귀 호출을 하지 않아도 그냥 바로 리턴이 가능하다.
위 코드에서 보면 아시겠지만 같은 인자(n=36)에 대해 아까 전 재귀로 프로그램을 돌렸을 때와 비교해보면, 8초 정도 나오던 것이 0.0초가 되어, 이는 굉장한 차이가 난다는 것을 알 수 있습니다.
1-5. bottom-up method
두번째 방식은 상향식 방법입니다. 이 접근법은 이름 그대로 아래에서 위로 올라가는 방식입니다.
그렇기 때문에 일반적으로 하위 문제의 "크기"에 대한 본질적인 개념에 의존하기 때문에 특정 하위 문제를 푸는 것은 "작은" 하위 문제의 해결에만 의존하게 됩니다.
우리는 이 방식을 사용할 때, 크기별로 하위 문제를 분류하고 가장 작은 문제부터 크기 순서로 해결합니다.
특정 하위 문제를 해결할 때, 우리는 문제의 solution이 의존하고 있는 모든 작은 하위 문제를 이미 해결했고, 그것들에 대한 solution들을 저장하였습니다.
즉 쉽게 말해, 제일 작은 size인 f(1)부터 시작하여 f(2), f(3), ... 이런 식으로 차근차근 올라가면서 푸는 방법입니다.
def fibonacci_bu(n):
memo = [0, 1] # base case
for i in range(2, n+1):
memo.append(memo[i - 1] + memo[i - 2])
return memo[-1]
print(fibonacci_bu(36))
1-6. top-down vs. bottom-up
두 개의 방식을 찬찬히 살펴보면 알겠지만 top-down은 이름 그대로 위에서부터 아래로 내려오면서 푸는 것이고 bottom-up은 아래에서 위로 올라가면서 풀어나갑니다.
또 둘의 특징으로, top-down은 위에서부터 시작하기 때문에 재귀로, bottom-up은 아래에서부터 시작하기 때문에 for 반복문으로 구성되어있기도 합니다.
그렇다면 둘 중에 뭐가 더 좋은 방법일까요?
예상하셨겠지만 결론부터 얘기 하자면 문제에 따라 다릅니다 (case by case). 그러나 일반적으로 사용되는 방식들의 특징을 비교해 보자면 아래 글과 같습니다.
실제로 보통 하향식(top-down)을 사용할 수 있다면 상향식(bottom-up)도 사용할 수 있지만, 필요한 값들이 필요할 때 적절한 순서로 함수 값을 계산하도록 주의해야 합니다.
top-down 동적 프로그래밍에서는 알려진 값(known values)을 저장하고 bottom-up 동적 프로그래밍에서는 사전 계산(precompute)을 합니다.
그렇기 때문에 사람들은 보통 bottom-up 보다는 top-down을 선호하긴 합니다.
1-7. 정리
- 자연적스러운 solution의 기계적 변형(mechanical transformation).
- 좀 더 자연스럽게 문제 해결 가능
- 하위 문제를 계산하는 순서는 스스로 알아서 한다.
- 계산 순서를 스스로 알아서 해결
- 우리는 모든 하위 문제들에 대한 답을 다 계산할 필요가 없을지도 모름.
- 모든 subproblem에 대한 답을 계산할 필요가 없다.
※ 별개 이야기로 주어진 size의 문제를 더 작은 size의 문제로 나누는 것을 recurrence equation(되풀이 방정식)이라고 합니다.
1-8. 관련된 문제
2748번: 피보나치 수 2
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net

def fibonacci_td(n):
if n < 2:
return n
if _memo[n] is None:
_memo[n] = fibonacci_td(n-1) + fibonacci_td(n-2)
return _memo[n]
_n = int(input())
_memo = [None] * 91
print(fibonacci_td(_n))
1-9. Rod cutting (막대 자르기) 문제
Serling Enterprises(철강 회사)는 긴 강철 막대(rod)를 구입하여 더 짧은 막대로 잘라 판매합니다.
막대를 자르는 데 드는 비용은 없습니다. 이 회사의 경영진들은 수익을 내기 위해 막대를 절단하는 가장 최고의 경우을 알고 싶어합니다.
Rod cutting 문제는 다음과 같습니다. 길이가 n인치인 막대와 i = 1, 2, ..., n에 대한 가격표 p_i가 주어지면 막대를 잘라내고 그 조각을 판매하여 얻을 수 있는 최대 수익 r_n을 결정합니다.

위 표와 같이 막대의 길이에 따라 시장 가격이 정해져 있습니다. 그렇다면 철강회사에서는 막대를 어떻게 자르는 것이 가장 돈을 많이 버는 방법일까요?

위 그림과 같이 어떻게 나눠서 파느냐에 따라 받을 수 있는 가격이 모두 다릅니다. 그렇다면 n인치의 철봉이 주어졌을 때 어떻게 나눠서 팔아야 가장 수익이 많이 나는지 알아보겠습니다.
여기서 이러한 최댓값을 구하는 것과 같은 구조의 문제를 Optimization Problem(최적화 문제)이라고 합니다.
- 그리고 optimization 문제는 대부분 DP로 해결합니다.
더 일반적으로, 우리는 더 짧은 막대로부터 오는 최적의 수익 관점에서 n >= 1에 대한 r_n 값을 프레임화할 수 있습니다:

- rn: n인치에서 얻을 수 있는 최대 수익
- pn: n인치짜리를 자르지 않은 통째로의 시장 가격
- 더해서 n인치가 나오는 총 n가지 경우에 대해 조사를 해서 최대값을 구한다.
- r1 + rn-1 은 사실상 p1 + rn-1 과 같다.
- 그래서 앞에 더해지는 r_n을 모두 p_n으로 대치하여 진행하는 것이 더 편하다.
이 문제는 재귀 구조를 배치하는 방식과 관련이 있지만 우리는 여기서 약간 더 간단한 방법으로 분해(decomposition)작업을 '왼쪽 끝을 잘라낸 첫 번째 길이 i와 오른쪽 나머지 길이 n-i로 구성된 것'으로 보기로 합시다.
첫 번째 조각이 아닌 나머지 부분만 더 나눌 수 있습니다. 따라서 우리는 다음과 같은 방정식을 얻습니다.

p[i] + cut_rod(length - i)
예를 들어, 4인치짜리 막대인 경우에,
- p1 + r3 = 9
- p2 + r2 = 10
- p3 + r1 = 9
- p4 = 9
위 네 가지 경우 중에서 가장 큰 값이 r4로 결정 되어야 하므로 r4=10이 되겠네요.
재귀 코드로 구현
import math
def cut_rod(length):
if length == 0: # r_0
return 0
max_revenue = -math.inf # -infinity
for i in range(1, length+1):
revenue = _price[i] + cut_rod(length-i)
if revenue > max_revenue:
max_revenue = revenue # 가장 큰 값을 저장하는 logic
return max_revenue
_price = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
_length = 8
print(cut_rod(_length))22
위와 같은의 재귀 방식의 CUT-ROD는 과연 효율적일까요?
당연히 그렇지 않습니다.
위 코드에서 발생하는 문제는 CUT-ROD가 동일한 매개 변수 값으로 자기 자신을 반복해서 호출한다는 점입니다.
- 동일한 하위 문제를 중복으로 해결하기 때문에 굉장히 비효율적인 계산이 됩니다.
- 그래서 이는 만약 코테 문제로 나왔다면 시간초과가 뜨게끔 했을 확률이 높겠죠?
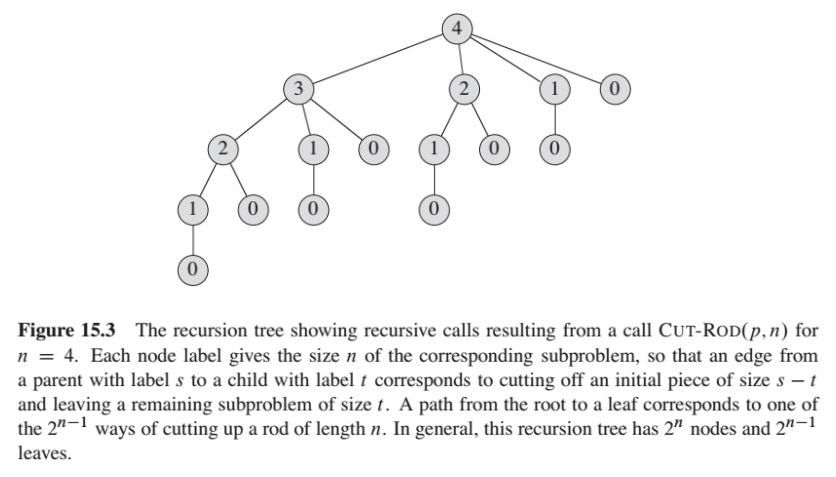
위 그림을 보기만 해도 0과 1에 대한 부분에서 엄청난 반복이 일어나는 것이 보이실 겁니다. 이는 이미 한번 계산한 건데도 그 때마다 다시 계산을 해야한다는 점에서 굉장히 비효율적인 것입니다. 특히 n의 크기가 커질수록 말이죠.
그렇기 때문에 이를 top-down 방식의 DP와 bottom-up 방식의 DP로 각각 바꾸어보겠습니다.
top-down with memoization 코드
def cut_rod_td(length):
if length == 0: # base case
return 0
if _memo[length] is None:
max_revenue = -math.inf
for i in range(1, length+1):
revenue = _price[i] + cut_rod_td(length-i)
if revenue > max_revenue:
max_revenue - revenue
# save r_i
_memo[length] = max_revenue
return _memo[length]
_price = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
_memo = [None] * 11
_length = 8
print(cut_rod_td(_length))top-down 방식에서는 반복적인 재귀 호출을 하되 memo를 활용하는 방식입니다.
bottom-up method 코드
def cut_rod_bu(length):
for i in range(1, length+1):
max_revenue = -math.inf
for j in range(1, i+1):
revenue = _price[j] + _memo[i-j] # memo를 활용함
if max_revenue < revenue:
max_revenue = revenue
# save r_i
_memo[i] = max_revenue
return _memo[length] # _memo[-1]
_price = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
_memo = [0] * 11
_length = 8
print(cut_rod_bu(_length))bottom-up 방식에서는 for문을 돌면서 memo를 계속 채워 넣는 방식으로 진행됩니다. 이때, 보통 재귀 호출 대신 memo 테이블에 해당하는 값이 들어가게 된다는 점이 중요한 사실입니다.
1-10. Elements of dynamic programming (동적 프로그래밍의 원소)
우리는 일반적으로 동적 프로그래밍을 많은 optimization problem(최적화 문제)에 적용합니다.
- 다시 말해, n 크기의 문제를 더 작은 size의 문제로 나눕니다.

- n인치 짜리 막대가 주어졌을 때 가질 수 있는 최대 가격 -> r_n
- pi: i인치로 나누어서 팔았을 때의 가격
- r_(n-i): 남은 부분 즉, n-i인치에서 가질 수 있는 최대 가격(recursion)
최적화 문제에 동적 프로그래밍을 적용하기 위해 반드시 필요한 두 가지 핵심 요소
동적 프로그래밍을 적용하기 위해서는 반드시 아래 두 가지 요소가 만족해야 합니다.
- Optimal substructure (최적의 구조)
- divide-and-conquer의 조건과 똑같은 특성
- optimal solution에는 하위 문제에 대한 optimal 솔루션이 포함되어 있습니다.
- Overlapping subproblems (중복되는 하위 문제)
- divide-and-conquer와 구분을 짓는 차이점
- solution을 찾는 데는 동일한 하위 문제를 여러 번 해결해야 합니다.
- 항상 새로운 하위 문제를 생성하는 분할 정복 방식
우리는 일반적으로 동적 프로그래밍을 optimization problems에 적용하고 그 문제들은 여러 해결 가능한 solution들을 가질 수 있습니다.
각 solution은 값을 가지고 있으며, 우리는 optimal value(최적의 값)를 가진 solution을 찾는 것이 목표입니다. 그러나 최적의 값을 찾아내는 데에는 여러 솔루션이 있을 수 있기 때문에, 그러한 솔루션은 optimal solution이 아니라 그 문제에 대한 optimal solution이라고 여겨집니다.
- optimal value로 부터 optimal solution을 만들어나간다는 개념.
1-11. 4가지 단계
동적 프로그래밍(DP) 알고리즘을 개발할 때, 우리는 다음과 같은 네 가지 단계의 순서를 따릅니다.
- optimal solution의 구조(structure)를 파악합니다.
- optimal solution의 값(value)을 재귀적으로 정의합니다.
- optimal solution의 값을 계산합니다.
- 계산된 정보를 바탕으로 optimal solution을 찾습니다.
1~3단계는 문제에 대한 동적 프로그래밍 솔루션의 기초를 형성합니다. 솔루션 자체가 아니라 최적 솔루션의 값(value of optimal solution)만 필요한 경우 4단계를 생략할 수도 있습니다.
1-12. Reconstructing a solution (솔루션 재구성 - 문제 확장)
다음은 각 막대 크기 j에 대해 최대 수익 rj 뿐만 아니라 절단하게 될 첫 번째 조각의 최적 크기 sj값도 계산하는 앞선 문제에서 확장된 BOTTOM-UP-CUT-ROD입니다.
수정 사항:
if max_revenue < revenue:
max_revenue = revenue
_first[i] = j # 앞에거(j)를 얼마만큼 잘라야지 revenue를 얻을 수 있는지를 저장_memo = [0] * 11
_first = [0] * 11
_length = 8
print(cut_rod_bu(_length))
while _length:
print(_first[_length], end=' ')
_length -= _first[_length]- _first:
- 총 10인치짜리의 optimal value를 달성하기 위해서 앞에 것(j)을 얼마만큼(몇 인치로) 잘라야지 revenue를 얻을 수 있는지에 대해 앞에 값을 기록하는 용도 (r4의 경우 p2니까 2를 기록)
# length 8
22
2 6
#length 4
10
2 2
#length 6
17
6
#length 10
30
10length 6은 6 혼자 파는 게 제일 비싸니까 legnth 8에서 6이 쓰였구나! 라고 생각할 수 있는 것입니다.
1-13. DP와 관련된 문제 2
1932번: 정수 삼각형
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net



위 문제에서 optimal structure는 maxV(0, 0)에서 얻을 수 있는 최대값을 생각해 보면 됩니다.

import sys
sys.stdin = open('bj1932_in.txt', 'r')
n = int(input())
triangle = []
for _ in range(n):
triangle.append(list(map(int, input().split())))
for i in range(1, n):
for j in range(i+1):
if j == 0:
triangle[i][j] += triangle[i-1][j]
elif i == j:
triangle[i][j] += triangle[i-1][j-1]
else:
triangle[i][j] += max(triangle[i-1][j], triangle[i-1][j-1])
print(triangle)
print(max(triangle[n-1]))[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] # original triangle
[[7], [10, 15], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [20, 25, 20, 19], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [20, 25, 20, 19], [24, 30, 27, 26, 24]]
30- j = 0인 경우는 삼각형의 한 줄에서 가장 왼쪽에 있는 값이기 때문에 바로 위의 줄의 j = 0 값과 더한 값으로 치환합니다.
- j == i인 경우 즉, 삼각형의 한 줄에서 가장 오른쪽에 있는 값이기 때문에 바로 위의 줄의 j = i 값과 더한 값으로 치환한다.
- 위 두 경우가 아니라면 위 줄의 왼쪽 branch와 오른쪽 branch로부터 둘 다 올 수 있는 경우인데, 이 때는 두 값의 max 값을 취해서 더해 주면 된다.
그런데 이를 만약 재귀를 통해 풀었다면 아래와 같이 시간초과가 발생하게 됩니다.
def max_path(row, col):
if row == _size - 1: # 제일 밑에 줄인 경우는 그냥 그 자리의 값이 결과값임
return _triangle[row][col]
path_left = _triangle[row][col] + max_path(row+1, col)
path_right = _triangle[row][col] + max_path(row+1, col+1)
return max(path_left, path_right)
_triangle = []
_size = int(input())
for _ in range(_size):
_triangle.append(list(map(int, input().split())))
print(max_path(0, 0))
- 한 줄 내려갈 때마다 중복 많아서 백준에 제출하면 시간초과가 발생합니다.
- 그렇기 때문에 DP로 풀어야 하는 문제입니다.
- Top down의 경우 triangle과 크기가 완전히 똑같은 memo list 하나를 만들고 max_path 함수를 호출했을 때 memo에 저장되어 있는지를 확인 후 저장이 안 되어 있다면 함수를 실행하도록 하고 저장이 되어 있다면 그냥 그 값을 리턴하도록 합니다.
- Bottom up의 경우 loop를 사용하여 밑에서부터 위로 계산하면서 올라가면 됩니다.
import sys
sys.stdin = open('bj1932_in.txt', 'r')
def max_path(row, col):
if row == _size - 1:
return _triangle[row][col]
if _memo[row][col] is None:
path_left = _triangle[row][col] + max_path(row + 1, col)
path_right = _triangle[row][col] + max_path(row + 1, col + 1)
_memo[row][col] = max(path_left, path_right)
return _memo[row][col]
_triangle = []
_memo = []
_size = int(input())
for _ in range(_size):
_triangle.append(list(map(int, input().split())))
_memo = [[None]*i for i in range(1, _size+1)]
print(max_path(0, 0))
print(_memo)30
[[30], [23, 21], [20, 13, 10], [7, 12, 10, 10], [None, None, None, None, None]]이 코드의 구조를 잘만 기억하고 계신다면 top-down 방식을 어디에도 적용하실 수 있을 겁니다.
1-14. 0-1 Knapsack problem (배낭 문제)
0-1 배낭 문제는 다음과 같습니다.
"가게를 털고 있는 도둑은 n개의 물건을 발견하게 됩니다. i번째 아이템은 vi 달러만큼의 가치가 있고 무게는 wi이며, 여기서 vi와 wi는 정수입니다. 도둑은 가능한 많이 귀중한 아이템들을 훔치고 싶어하지만, 그가 가진 배낭에는 정수 W 만큼의 무게까지만 실을 수 있습니다. 그렇다면 그는 어떤 아이템들을 가져가는 것이 최선의 방법일까요?"
이 문제를 보시면 알겠지만 이 또한 최댓값을 구하는 최적화 문제(optimization problem)입니다.
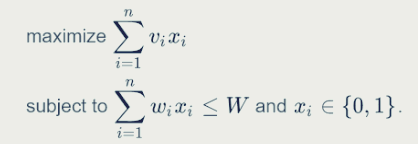
- objective function: 무언가를 최대화(maximize) 해야하는 함수
- 총 가져가는 물건의 가치는 vi · xi 를 모든 i에 대한 값을 모두 더한 값이다.
- constraint(제약 조건): 최대화 할 때의 조건
- 담은 물건의 무게를 모두 더했을 때 W값을 넘어가면 안된다.
- xi 값은 물건을 담으면 1, 안 담으면 0으로 계산한다. (문제가 0-1 배낭인 이유)
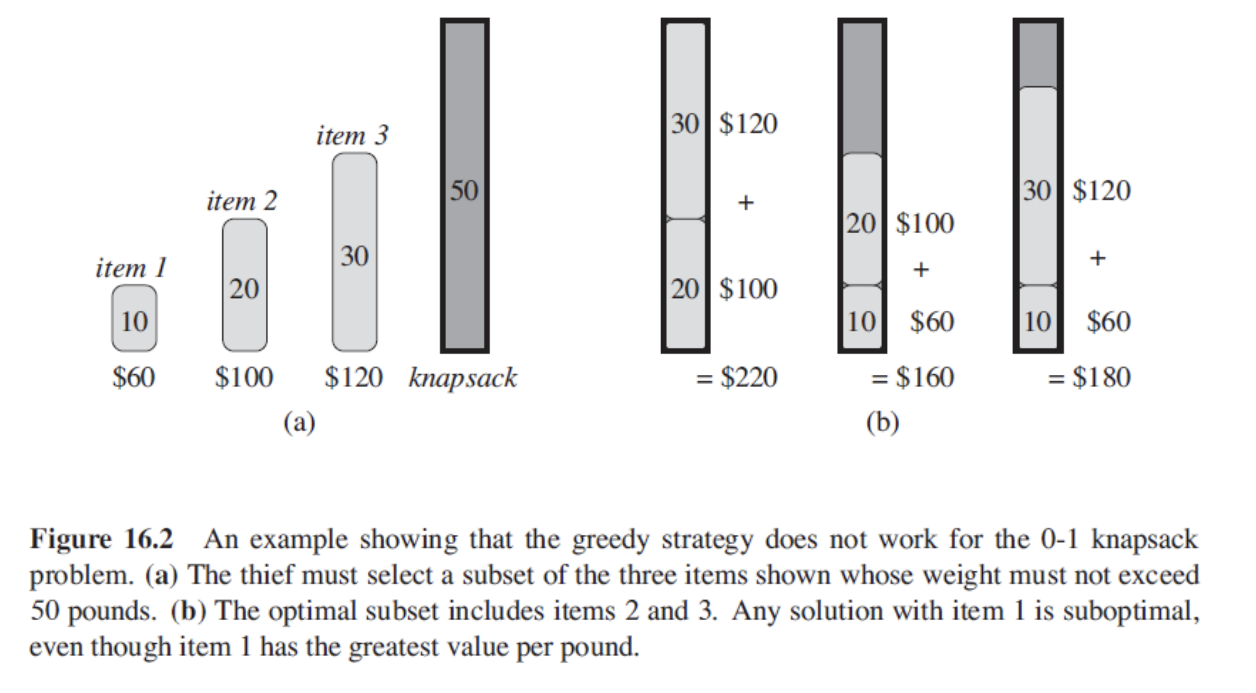
위 그림은 그리디 알고리즘으로는 0-1 배낭 문제가 풀리지 않을 것임을 보여줍니다.
(a): 도둑은 무게가 50 pounds를 초과하지 않으면서 3개의 아이템을 골라야하는 상황을 보여주는 그림입니다.
(b): 최적의 선택지는 2번 아이템과 3번 아이템을 포함하는 것입니다. 1번 아이템을 가진 어떠한 솔루션은 최적의 솔루션이 될 수 없으며, 심지어 1번 아이템이 모든 아이템들 중 제일 무게당 가격이 제일 비쌈에도 불구하고 최적의 솔루션이 아니라는 점은 그리디로는 풀릴 수 없다는 것을 보여줍니다.
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net


- maxV(7,0) - 여유공간 7, 고려하는 0번째 물건
재귀 코드로 구현
def knapsack(capacity, item):
# capacity: current capacity of the knapsack, [0.._capacity]
# item: index of the item to be considered, [0..number-1]
# _number: number of items -> W
# _capacity: capacity of the knapsack -> W
# _weight: weight list of the items -> Wi
# _value: value list of the items -> Vi
if capacity == 0 or item >= _number:
return 0
if _weight[item] > capacity: # 아이템의 무게가 현재 수용 가능한 무게 이상인 경우
return knapsack(capacity, item+1) # 그 다음 아이템 고려
with_the_item = _value[item] + knapsack(capacity - _weight[item], item+1)
without_the_item = knapsack(capacity, item+1)
return max(with_the_item, without_the_item)- knapsack(-capacity, 0)


- Top down으로 바꾼다.
- 이때, memo를 리스트가 딕셔너리로 만들어서 튜플 형태의 노드를 key로 해서 값을 계속 저장한다.
- key: (capacity, item) | value: value
- 재귀 호출을 할 때, memo안에 존재하는 지를 먼저 파악해서 그걸 토대로 다음 행동을 결정하면서 진행한다.
- 저장해야 하는 key 수가 그렇게 많지 않음
- 이때, memo를 리스트가 딕셔너리로 만들어서 튜플 형태의 노드를 key로 해서 값을 계속 저장한다.
- bottom up으로 바꾼다.
- 어디서 부터 올라가야 될 지를 알 수가 없기 때문에 이차원 리스트의 사이즈가 W x N 만큼으로 다 채워지므로 불필요한 계산을 많이하게 되어 실행 속도가 굉장히 오래 걸릴 것이다.

따라서 왼쪽으로 가서 물건을 집어 넣으면 capcity에서 물건의 weight 만큼 뺀 후 다음 아이템에 대해 knapsack 함수를 재귀 호출을 진행한다.
import sys
def knapsack(capacity, item):
# capacity: current capacity of the knapsack, [0.._capacity]
# item: index of the item to be considered, [0..number-1]
# _number: number of items -> N
# _capacity: capacity of the knapsack -> W
# _weight: weight list of the items -> wi
# _value: value list of the items -> vi
if capacity == 0 or item >= _number:
return 0
if _memo.get((capacity, item), None) is None:
if _weight[item] > capacity: # 넣고 싶어도 못넣는 경우
return knapsack(capacity, item + 1) # 만약 현재 item이 용량을 넘어서면 다음 item 보기
with_the_item = _value[item] + knapsack(capacity - _weight[item], item + 1)
without_the_item = knapsack(capacity, item + 1)
_memo[(capacity, item)] = max(with_the_item, without_the_item)
return _memo[(capacity, item)]
sys.stdin = open('bj12865_in.txt')
input = sys.stdin.readline
_number, _capacity = map(int, input().split()) # n: 갯수, k: 버틸 수 있는 무게
_memo = {}
_weight = []
_value = []
for i in range(_number):
w, v = map(int, input().split())
_weight.append(w)
_value.append(v)
print(knapsack(_capacity, 0))
print(_memo)14
{(3, 2): 6, (7, 3): 12, (7, 2): 12, (7, 1): 14, (7, 0): 14}
top-down 방식답게 기존의 재귀 코드에서 memo를 확인하는 if문이 추가되었고, 현재의 아이템을 취한 경우와 아닌 경우에 대해 max값을 구하여 memo에 추가하는 식의 코드입니다.
당신이 좋아할만한 콘텐츠
-
[자료구조와 알고리즘 | 파이썬] Shortest Path Algorithms(최단 거리 알고리즘) & Dijkstra Algorithm(다익스트라 알고리즘) & Bellman-Ford Algorithm(벨만-포드 알고리즘) + 위상 정렬(Topology sort) 2022.12.31
-
[자료구조와 알고리즘 | 파이썬] Greedy Algorithms(그리디 알고리즘) 2022.12.31
-
[자료구조와 알고리즘 | 파이썬] Heaps (힙) 자료구조 2022.12.31
-
[자료구조와 알고리즘 | 파이썬] Graphs - 그래프 자료구조(+약간의 python 개념) 2022.12.31
소중한 공감 감사합니다