[자료구조와 알고리즘 | 파이썬] Recursion and Backtracking(재귀 & 백트래킹) + Divide and Conquer(분할정복) 알고리즘
2022.12.31- -
1. Recursion
우리는 목표를 달성하기 위해 어떠한 메소드 안에서 또 다른 메소드를 호출할 수 있다는 사실을 알고 있습니다. 이와 유사하게 메소드는 자기 스스로 또한 호출할 수 있습니다.
Recursion(재귀) 방식은 programming technique 중 하나로 어떤 메소드가 목적을 달성하기 위해서 본인 스스로를 호출할 수 있는 메소드를 말합니다.
두 가지 접근 to repetitive algorithms(반복 알고리즘)
iteration(순회)
- loops(for, while, do-while)
recursion(재귀)
- Function calls itself
- 즉, 함수가 자기 자신을 계속해서 반복하여 호출하는 방법
- 문제를 breaking down 하기에 적절한 방식
- break down: 주어진 문제를 더 작은 크기의 문제로 줄이는 행위
- break down: 주어진 문제를 더 작은 크기의 문제로 줄이는 행위
- 많은 경우에 알고리즘을 대폭 단순화시킨다.
- 어떤 문제를 해결하려 할 때 그 문제에 recursion을 적용할 수 있는 경우가 있고 아닌 경우가 있는데, 만약 적용할 수 있는 경우에 그 문제를 엄청나게 간단하게 만들어 준다.
1-1. Iterative factorial algorithm(순회 팩토리얼 알고리즘)

def factorial(n):
if n == 0:
return 1
else:
ans = n
for i in range(n-1, 0, -1):
ans *= i
return ans
num = 7
print("%d! = %d" % (num, factorial(num)))7! = 5040단순히 반복문을 통해 팩토리얼을 계산하는 문제입니다.
1-2. Recursive factorial algorithm(재귀 팩토리얼 알고리즘)

위 식처럼 재귀 방식으로 팩토리얼 문제를 단순화 시킬 수 있습니다. Factorial(n)은 n을 1씩 줄여가며 현재의 n과 곱하는 것이 반복됩니다.
def factorial(n):
# test for a base case
if n == 0:
return 1
# general case (calculation and recursive call)
else:
return n * factorial(n-1) # 함수가 자기 자신을 다시 호출
num = 7
print("%d! = %d" % (num, factorial(num)))7! = 5040
recursive 함수의 핵심은 두 가지 경우가 존재해야 한다는 것입니다.
- Baes cases: 계산을 안 해도 한번에 답이 바로 나오는 경우(위의 factorial 예시에서 n = 0 일 때 1 인 상황)
- 이는 회귀의 종료를 말하며, 회귀가 기본 조건을 만족하기만 하면 멈추게 될 것을 의미합니다.
- 사실상 이 부분은 계산이 필요한 것이 아니라 미리 정해진 정의에 가깝습니다.
- Recursive cases: 함수 호출을 종료 시킬 수 있는 조건이 있는 경우
- 함수가 자기 자신을 호출하여 기본 조건(base cases)을 성취하는 방향으로 진행하는 것입니다.
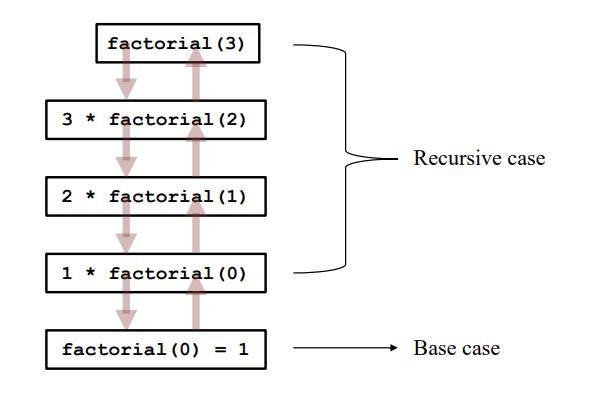
위 사진을 보면, 메모리에 함수 object는 최대 4개가 올라가지만 각자의 재귀 호출이 종료된 후에는 메모리가 삭제됩니다.
그래서 recursion은 호출하는 횟수만큼 memory를 많이 잡아 먹는다는 문제도 있습니다.
1-3. Example: power function(멱 함수)
수학에서 멱함수는 거듭제곱의 지수를 고정하고 밑을 변수로 하는 함수를 말합니다.
예를 들어, 23 이 8이기 때문에 다음은 8과 동일한 result2의 값을 설정할 것입니다:
- result2 = power(2, 3)
power function의 정의는 다음 공식에 기반합니다.
- xn is equal to xn-1 * x
- break down 가능(반복되기 때문)
- recursive case에 해당(base case가 존재)
n = 0, 즉 stopping case의 경우, 만약 n = 0이면 power(x, n)은 단순히 1을 반환합니다.(x0 = 1 이기 때문.)
- base case 존재! -> 회귀 사용 가능!
따라서 power()도 recursive로 구현할 수 있는 조건을 만족합니다.
def power(base, exponent):
if exponent == 0:
return 1
else:
return base * power(base, expoenet-1)
a, b = 5, 3
print("%d**%d = %d" %(a, b, power(a, b)))5**3 = 125
1-4. Complexity of recursive algorithms
recursive algorithm의 order(차수)를 정의하는 것은 recursion의 order를 결정하는 문제와 그 문제의 recursive method body의 order를 곱하는 것에 대한 문제입니다.
- 즉, 재귀 호출 횟수 x 재귀 문의 line 갯수
power 함수를 실행했을 때 running time f(n)은 어떻게 되는지 보겠습니다.
def power(base, exponent): # f(n)
# c
if exponent == 0:
return 1
# f(n-1)
else:
return base * power(base, expoenet-1)
a, b = 5, 3
print("%d**%d = %d" %(a, b, power(a, b)))f(n) = c + f(n-1) // n = n - 1을 계속 대입한다 + c는 하나씩 계속 늘어날 것임
= 2c + f(n-2)
= ic + f(n-i)
= n*c + f(0)
따라서 O(n)을 갖는다. (이 예제의 경우, for loop와 동일한 O(n))

따라서 body는 O(1) (위에서는 c로 표현함)이고 recursion은 O(n)만큼 반복이기 때문에 전체 algorithm의 order는 O(n) 이다.
2. Divide and Conquer(분할 정복) 알고리즘
Divide and conquer (분할 및 정복)란,
- algorithm design paradigm(방법) - 즉, 하나의 알고리즘 디자인 패러다임입니다.
- based on multi-branched recursion - 여러 갈래의 재귀에 기반합니다.
앞서 다루었던 fatorial을 recursion으로 풀었던 문제는 single-branched recursion이라고 볼 수 있겠습니다.

Divided-and-conquer technique (typical case)

분할 정복은 다음과 같은 과정으로 진행됩니다.
- 어떤 문제를 풀 때, size가 n인 문제를 n/2인 문제 두 개로 나눈다.(recursion)
- 또 다시, 방금 나눈 두 문제를 n/4 짜리 문제 4개로 나누고 -> 또 둘씩 나눠지는 것이 반복된다.
- 그래서 나누어져서 size가 작아진 문제들을 하나씩 해결한다.
- 위 사진의 방법은 2-branched-recursion임. (두 갈래로 나뉘기 때문)
2-1. divide-and-conquer approch (분할 정복 접근)
- 몇가지의 original problem과는 유사하지만 size는 더 작은 subproblem들로 쪼갠다.(Divide - 분할)
- 각각의 subproblem들을 recursively(재귀적으로) 해결한다.(Conquer - 정복)
- 그 후, original problem을 해결하기 위한 solution을 만들기 위해 위 결과로 나온 solution들을 결합한다.
(Combine - 결합)
정리하자면, The divide-and-conquer 패러다임은 다음과 같은 세 가지 단계(recursion의 각 레벨)를 수반한다고 생각하면 됩니다.
- 같은 문제의 더 작은 instances의 수많은 sub-problem들로 Divide 한다.
- 그들을 재귀적으로 풀어냄으로써 작은 문제들을 정복한다.
- 작은 문제들에 대한 솔루션을 결합하여 original problem에 대한 솔루션을 만들어낸다.
2-2. Divide-and-conquer to find the maximum (최댓값 찾기)
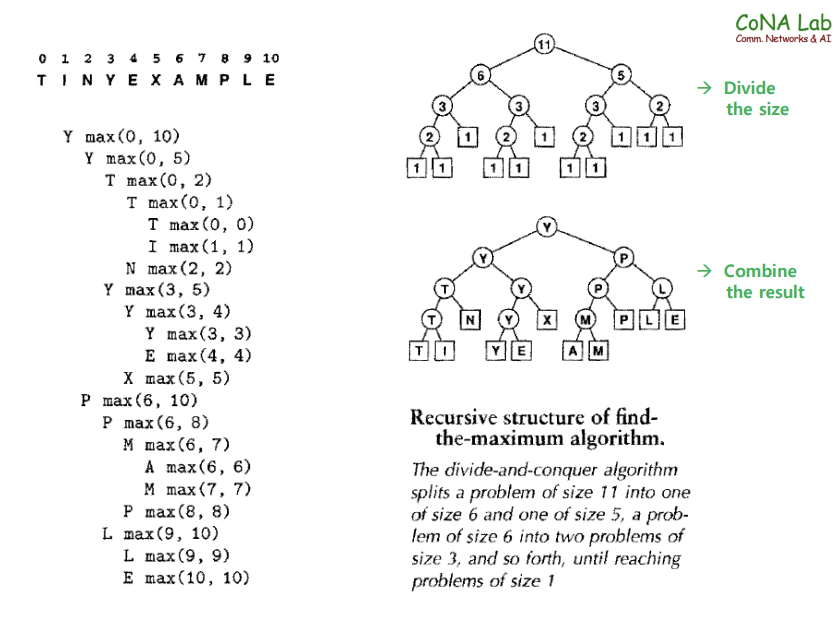
def find_max(data, left, right):
# base case(계산이 필요없는 base case, 원소가 하나있는 경우이므로 그냥 반환)
if left == right:
return data[left]
#recursive case
mid = (left + right) // 2
x = find_max(data, left, mid) # left branch(list)
y = find_max(data, mid+1, right) #right branch(list)
#combine
if x > y:
return x
else:
return y
a = list("TINYEXAMPLE") # a = ['T', 'I', 'N' ,..., 'E']
print(find_max(a, 0, len(a)-1))Y저도 처음에 위 알고리즘을 이해하기 위해서 굉장히 오랜시간이 걸렸는데 말을 길게 풀어서 설명을 해 보겠습니다.
- 먼저, 크기가 1인 리스트는 그냥 그 원소를 리턴하면 되니까 (즉, base case니까) 크기가 1인 리스트에 대해서는 가장 먼저 처리를 합니다.
- 그리고 만약에 리스트의 크기가 (2, 1)과 같이 나눠졌으면 '2' 부분은 또 다시 (1,1) 로 나누어 질 것이기 때문에 각각이 x, y에 들어가서 비교를 한 뒤에 더 큰 걸 반환하게 됩니다.
- 그 후 호출했던 (2, 1)로 올라가서 (1,1)을 비교하여 큰 알파벳과 '1' 부분의 알파벳을 다시 비교하여 더 큰 쪽을 다시 반환해서 또 그 위에 해당하는 (2,1)을 호출한 곳으로 올라가서 비교하고 비교하고 비교하고........ 하는 방식입니다.
다시 쉽게 설명하자면, x, y의 값은 계속해서 재귀 호출이 진행되면서 left branch와 right branch로 분기되는데
그 때마다의 왼쪽 리스트의 max값과, 오른쪽 리스트의 max값을 의미하게 됩니다.
그래서 현재 돌고 있는 left-list의 max값이 정해지면 그 다음은 right list의 y을 알아내야 하기 때문에 그 다음 찾아야 하는 리스트의 범위를 mid+1, right으로 지정하여 재귀 호출을 하는 것입니다.
2-3. 분할정복의 큰 틀
<psuedo code>
function F(x):
if F(x)의 문제가 간단 then :
return F(x)를 직접 계산한 값
else:
x를 y1, y2로 분할
F(y1);
F(y2);
return F(y1), F(y2)로부터 F(x)를 구한 값; 즉 문제의 정의!!큰 문제를 2개 이상의 작은 문제로, 즉 y1과 y2로 나누고 만약 y1 또는 y2가 바로 계산할 수 있다면 (base case의 경우) 계산한 값을 반환함으로써 작은 문제를 하나 씩 해결해 나가면서 큰 문제를 해결할 수 있습니다.
위 코드는 분할 정복이나 재귀 문제를 구현하기 전에 미리 짜 보면 좋은 psuedo code 입니다.
어떤 문제를 위와 같이 먼저 구성해 보면 좋은 것이 여기서 DP(다이나믹 프로그래밍)로도 파생이 되는 경우 약간만 수정하면 적용이 됩니다.
또한 재귀, 백트래킹, 분할 정복에서 가장 중요하고 가장 먼저 생각해야 하는 것은 base case를 찾는 것임을 명심합시다.
Q) size에 따라 iterative 방법과 recursive 방법이 더 좋은 것이 있을 것인데 이를 어떻게 판단하는가?
A) 각각의 장단점이 존재하고 무엇을 쓸 지에 대한 명확한 기준은 없으나 프로그래머가 판단했을 때 몇 줄만에 코드가 끝나고 size가 적당하다면 recursive를 사용하지만 data의 size가 너무 크면 iterative를 사용한다.
3. The Towers of Hanoi (하노이의 탑)
다음으로 볼 예제는 재귀의 교과서라고 볼 수도 있는하노이의 탑입니다.
관련된 백준 문제 또한 있습니다.
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
하노이의 탑 문제는 다음과 같습니다.

우선 막대기 세 개가 존재합니다. 왼쪽부터 source(출발), extra(경유), destination(도착) 으로 지칭하겠습니다.
이 수수께끼의 목표는 source(first) 막대에 모여있는 원반을 destination(third) 막대로 모두 옮기는 것이라고 볼 수 있습니다. 즉, 우리가 달성해야 할 과업인 것입니다.
우리는 이때 "extra"라는 중간에 놓인 막대를 잠시 둘 수 있는 임시 공간(경유 역할)으로 사용할 수 있습니다.
이 알고리즘을 풀 때는 다음 세 가지 규칙을 반드시 준수해야 합니다.
- 한번에 하나의 disk 만을 옮길 수 있다.
- 한 원반 위에 그것보다 크기가 큰 disk를 놓을 수 없다.
- 모든 원반들은 3개의 막대 중에 한개의 막대 위에 있어야 한다.
먼저, recursive(재귀)로 해결하기 위해 제일 간단한 경우(base case)부터 생각해 보겠습니다.
3-1. 1-disk & 2-disk cases(원반이 하나인 경우 & 두개인 경우) - base case
base case 1. 원반이 하나인 경우
source -> destination으로 원반을 한번만 움직이면 됩니다.
그래서 총 1번의 이동이 요구되고, 이는 계산이 필요없는 base case에 해당합니다.
base case 2. 원반이 두 개인 경우

- source -> extra으로 원반을 한번 이동한다.
- source -> destination으로 원반을 한번 이동한다.
- extra -> destination으로 원반을 한번 이동한다.
총 3번의 이동이 요구됩니다.
3-2. 3개의 원반을 이동시키는 경우 - f(3)

- 가장 아래 깔린 제일 큰 원반을 C로 옮기기 위해서는 가장 먼저 그 위에 있는 두 개의 원반을 extra로 옮겨야 한다.(f(2) 사용 - 3 step)
- 이 경우 extra를 destination으로 생각하고 진행한다.
- 그러면 source에 제일 큰 거가 하나가 남는데 이는 base case이다. (1 step)
- extra로 옮겨놨던 두 개를 다시 dest로 옮긴다.(f(2) 사용 - 3 step)
그래서 각 과정의 이동수를 더해보면 총 7번의 이동이 요구됩니다.
- f(3) = f(2) + 1 + f(2) = 3 + 1 + 3 =7
그렇다면 만약 7개의 disk가 있다고 생각해 봅시다.
- f(7) = f(6) + 1 + f(6)
- f(6) = f(5) + 1 + f(5)
- ...
- f(2) = f(1) + 1 +f(1)
- f(1) = 1
위와 같이 단순화가 가능해졌습니다.
3-3. Recursive algorithm design
- (n-1)개의 원반을 source -> extra 로 이동 -> recursive case
- 1개의 원반을 source -> destination -> base case (가장 큰 원반 옮기는)
- (n-1)개의 원반을 extra-> destination로 이동 -> recursive case

코드로 구현(recursion, 하노이 탑)
def hanoi(disks, src, dst, extra):
if disks == 1:
hanoi.count += 1
print(f'{hanoi.count}: move from {src} to {dst}') #formatted printing
else:
# f(n-1)
hanoi(disks-1, src, extra, dest) # 제일 큰 원반 위의 n-1개의 원반들을 extra로 옮김
# 1
hanoi.count += 1 # 제일 큰 원반 하나를 dst로 옮김
print(f'{hanoi.count}: move from {src} to {dst}')
# f(n-1)
hanoi(disks-1, extra, dst, src) # extra의 원반들을 dst로 모두 옮김
hanoi.count = 0 #static variable of hanoi()
hanoi(3, 1, 3, 2)
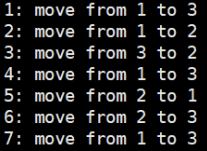
hanoi()가 호출되는 횟수 만큼 호출 스택이 쌓이고 각 함수의 지역 변수도 그만큼 존재하게 되는데 hanoi.count와 같이 static 변수로 선언하게 되면 파이썬에서는 모든 hanoi() 함수 object에서 같은 변수를 공유하게 됩니다.
즉 각 함수에서 해당 변수를 참조할 때는 그 변수로 참조하겠다는 의미입니다.
그래서 하나의 hanoi() 함수에서 count 값을 바꾸면 모든 hanoi() object에서도 현재 참조 중인 count 변수가 같기 때문에 변한 값으로 사용하게 됩니다.
N개의 원반의 스택을 가진 이 퍼즐을 풀기 위해서는 2N-1 개의 각각의 원반의 이동을 만들어내야 합니다. 따라서, 하노이의 탑 알고리즘은 원래 O(2n) 의 시간 복잡도를 갖습니다.
f(n) = 2f(n-1) + 1
= 22f(n-2) + 2+ 1
= 23f(n-3) + 22 + 2 + 1
= 2if(n-i) + 2i-1 + 2i-2 + ... + 1
= 2if(n-i) + 2i - 1
= 2n-1f(1) + 2i - 1
= 2n - 1
만약 1초당 하나 씩 disk를 옮긴다고 했을때, n=40인 경우 적어도 다 끝내기 위해서 348 세기나 걸리게 됩니다.(상상도 안 되죠...?)
4. Backtracking(백트래킹) 알고리즘
- Backtracking techqniue
- Backtracking paradigm
- Backtracking method
- Backtracking algorithm
백트래킹 알고리즘은 단순 알고리즘이라고 불릴 뿐 아니라 위와 같이 다양한 용어로 불립니다.
4-1. Brute-force algorithm(완전 탐색 알고리즘)
- Brute-force search or exhaustive search
백트래킹을 알기위해선 먼저 브루트포스 또는 완전 탐색에 대해서 먼저 알아야 합니다. 이는 매우 광범위하게 적용되는 문제 풀이 테크닉입니다. 보통 초보자가 코딩 문제를 푸는 문제이기도 하죠.
완전 탐색이란, solution에 대해 가능성 있는 모~든 후보들을 시스템적으로 나열하고 각 후보들이 problem의 상태를 만족하는지 아닌지 판별하는 알고리즘입니다.
간단히 말해서 이름 그대로 무식하게 푸는 방식이라고 할 수 있습니다.(하지만 때론 무식하게 푸는 것이 쉽게 풀리는 경우도 많습니다.)
살면서 스도쿠를 한번씩은 해 보셨을 텐데요. 아래와 같은 스도쿠에 빈칸을 채우는데에는 9n 의 방법이 있습니다.
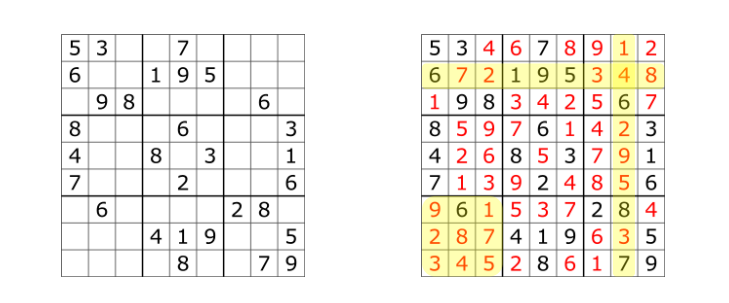
즉, 이 문제를 brute-force 기법으로 풀려면 9x9 size의 스도쿠 판의 각 칸마다 1~9까지의 수들을 전부 넣어 보면서 조건을 만족하는지 하나하나 확인해야 하는데, 이 경우에 시간 복잡도가 O(9n)이 나오게 됩니다.
그렇기 때문에 때에 따라서 브루트포스가 쓰이는 경우가 있기는 하지만, 스도쿠와 같이 일일히 하나하나 따졌을 때 굉장히 피곤한 경우에는 브루트 포스를 사용할 수가 없습니다.
그렇다면 어떤식으로 스도쿠 문제를 풀어나가야 할까요?
만약 첫 번째 칸에 1을 넣고 바로 다음 칸에 1을 넣는 경우 그 뒤는 볼 것도 없이 해당 경로는 스도쿠가 만족하지 않는 코드인 것입니다. 이 아이디어를 활용하여 경우를 잘 판단해서 다시 뒤(back)로 돌아갈 수 있는 방법을 찾아야 할 것입니다.
조금 뒤에서 다시 설명하겠지만 백트래킹이라는 이름이 이 이유로 붙게된 것입니다.
브루트 포스 코드로 구현 - 순열 문제
브루트 포스 알고리즘의 예시를 코드를 통해 살펴보겠습니다. 아래는 주어진 문자열 s와 길이 n에 대하여 가능한 모든 배치 방식을 생성하기 위한 recursive 접근 방식을 사용했습니다.
def bit_str(ans):
if len(ans) == n:
print(*ans)
else:
for s in data:
ans.append(s)
bit_str(ans)
ans.pop()
n, data = 3, 'abc'
bit_str([])위 문제는 길이가 3인 모든 수열을 반환하는 문제입니다.
- aaa, aab, aac, aba ,... , ccc
즉, 총 33 가지의 문자열을 모두 생성해 보는 것입니다.
위 코드 진행 방식
- 처음에 f([ ]) 가 호출되면, 아직 빈 리스트이기 때문에 else문이 실행되고 'abc'라는 data 중에서 첫 번째에 위치한 'a'에 대해 for문이 진행된다.
- for문
- 배열에 'a'를 추가
- f(['a'])에 대해 재귀호출을 진행
- else문으로 넘어가 또 다시 a에 대해 for문 진행.
- for문
- 그럼 배열에 'a'가 또 추가되고
- f(['a', 'a']) 가 호출됨.
- if를 아직까지도 만족하지 않기 때문에 또 else로 넘어가 또 a에 대해 for문이 진행되어 배열에 a가 추가되고 f(['a', 'a', 'a'])가 호출됨.
- 이 때는 if문을 만족하기 때문에 배열의 값을 모두 프린트 한다. ('aaa')
- if를 아직까지도 만족하지 않기 때문에 또 else로 넘어가 또 a에 대해 for문이 진행되어 배열에 a가 추가되고 f(['a', 'a', 'a'])가 호출됨.
- 여기서부터가 중요한데,
- 프린트를 하고 나서는 현재 함수가 종료되고 이 함수가 호출된 곳(['a', 'a', 'a'])으로 돌아간다.
- 호출된 곳에 돌아가자마자 있는 코드는 ans.pop()이므로 가장 마지막의 원소를 반환하면서 'a'에 대해 진행되던 for문은 그 다음 문자인 'b'로 넘어가서 b를 추가하고 aab에 대해서 해당 과정을 계속 진행하게 된다.
- 이를 도식화하면 다음과 같다.
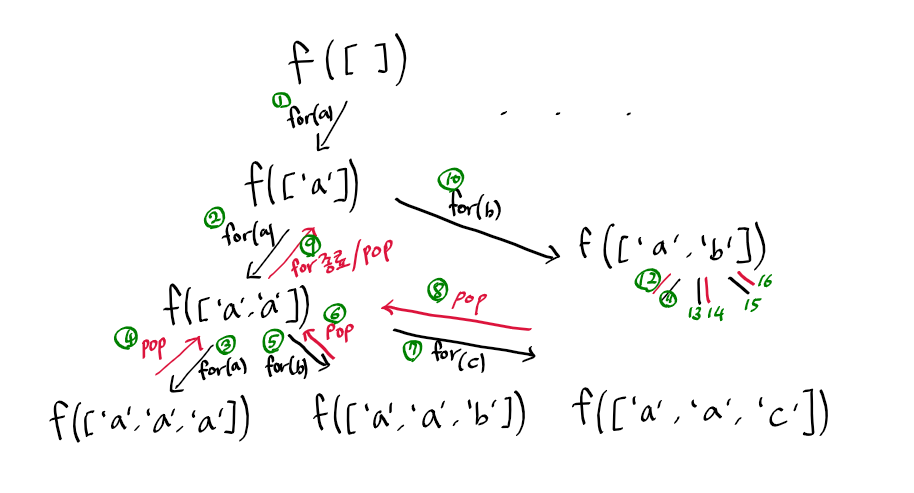
프로그래밍을 하다 보면 for loop보다 recursion이 오히려 더 좋다고 합니다.
이는 2중 for loop인 경우 코드가 더 간결할 수는 있지만, n의 size가 매우 커질 경우 코드가 시간 안에 돌아가지 않을 것이기 때문입니다.
4-2. Backtracking(백트래킹) 알고리즘
이제 브루트 포스가 어떤 것인지 알았으니 이를 기반으로 백트래킹에 대해서 자세히 살펴보도록 하겠습니다.
Backtracking은 traversing tree(트리 순회) 구조와 같은 문제의 유형에 특히 유용한 recursion의 한 형태인데, 각 노드에 대한 수 많은 옵션들이 제시된 곳에서 유용한 것입니다.
또한, Backtracking은 exhaustive searching(완전 탐색)을 위한 divide-and-conquer 방식이다. 여기서 중요한 점은 백트래킹은 결과를 낼 수 없는 가지들은 쳐낸다는 점입니다.
- 완전탐색을 위한 분할정복? -> 완전 탐색은 오래 걸리니 분할 정복이라는 툴로 시간을 줄임
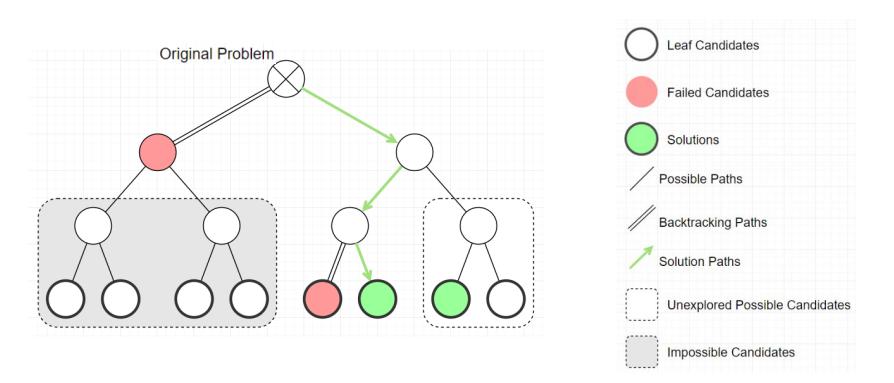
즉, 위의 그림처럼 가지를 모두 탐색하면서 조건을 일일히 따져보는 것이 아니라, 중간에 failed candidates(가망이 없는 후보)가 발견되면 다음 가지로 넘어가지 않고 다시 되돌아가(back) 현재 노드부터 다시 tracking을 시작하여 결과를 찾아내는 알고리즘인 것입니다.
즉 Failed Candidates 이후의 노드들은 어차피 볼 필요도 없다는 아이디어가 중요합니다.
아래는 3*3 스도쿠를 백트래킹 방식으로 구현한 것을 도식화 한 것입니다.
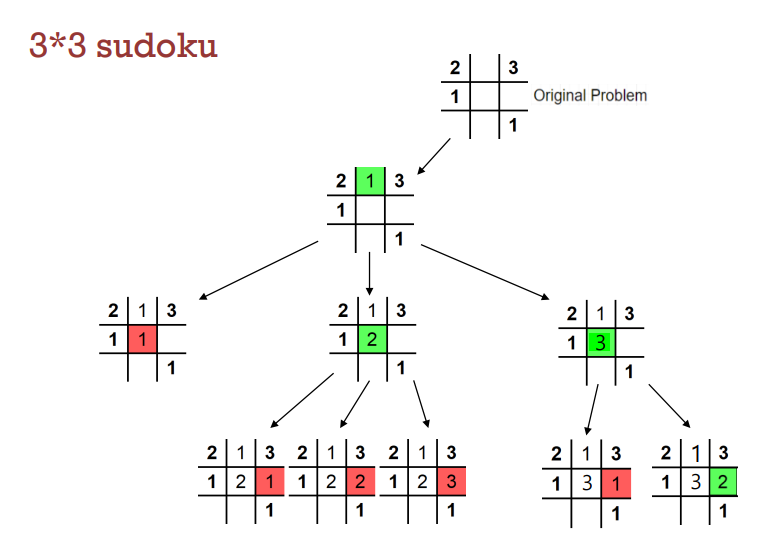
4-3. 관련된 문제
15649번: N과 M (1)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
def permute(ans):
if len(ans) == m:
print(*ans)
else:
for i in range(1, n + 1):
if i not in ans:
ans.append(i)
permute(ans)
ans.pop()
n, m = map(int, input().split())
permute([])3 2 // input
1 2
1 3
2 1
2 3
3 1
3 2
15650번: N과 M (2)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
def combine(ans):
if len(ans) == m:
print(*ans)
else:
for i in range(1, n + 1):
if (len(ans) >= 1) and (i <= ans[-1]):
continue
else:
ans.append(i)
combine(ans)
ans.pop()
n, m = map(int, input().split())
combine([])idea: n과m 1번 문제와 동일하게 돌긴 도는데 특정 부분(조건에 맞는)에서만 넘어가게 짜야 하기 때문에 그 특정 부분을 지정하는 것이 제일 중요합니다.
- 조건에 맞지 않으면 if문을 빠져나와 주는 back 작업을 진행합니다.
if문에서 반드시 배열의 길이를 먼저 check 하고 그 다음 i가 배열의 마지막보다 큰 지를 check해야 합니다.(순서 유의)
- 배열의 크기가 1보다 커야지 배열의 마지막이 존재할 것이기 때문
4 2 // input
1 2
1 3
1 4
2 3
2 4
3 4
팁) 조건문에서 되도록 '&'대신 'and'를 사용해야 하는 이유
>>> 0 < 1
True
>>> 0 < 1 & 3 < 2
True
연산자의 우선 순위(operator precedance)
- 부등호의 우선순위보다 '&'의 우선순위가 더 높아서 (1&3)을 먼저 계산하게 되어 0<1<2 라는 식이 되므로 예상치 못한 True가 나오게 됩니다.
그렇기 때문에 파이썬에서 두 조건을 비교하는 if문을 쓸 때는 and를 사용하도록 합시다.
'CS 지식 > 자료구조와 알고리즘(Python)' 카테고리의 다른 글
| [자료구조와 알고리즘 | 파이썬] Linked List(연결 리스트) | Singly linked list(단일 연결 리스트)와 Doubly linked list(이중 연결 리스트) (0) | 2022.12.31 |
|---|---|
| [자료구조와 알고리즘 | 파이썬] Sorting (정렬) (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Searching(탐색)과 Complexity(복잡도) + 빅오표기법 (1) | 2022.12.31 |
| [python] Python objects(객체)란? (0) | 2022.12.31 |
| [python] Python 기본 (0) | 2022.12.31 |
소중한 공감 감사합니다