[자료구조 | Java] LinkedList(연결 리스트) 이론 및 구현
2022.12.27- -
이번 포스팅은 지난 포스팅에 이어 ArrayList에서 했던 것과 마찬가지로 LinkedList에서의 데이터 삽입, 데이터 삭제, 리스트 검색 등의 기능에 대해서 다뤄보도록 하겠습니다.
1. 연결리스트(Linked List)란?
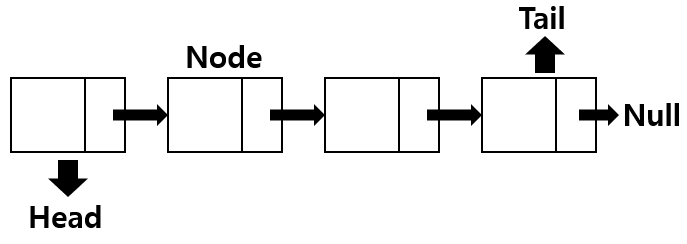
LinkedList는 Node라는 객체로 이루어져 있는데 Node는 데이터를 저장하는 field와 다음 노드를 가리킬 수 있는 next pointer field로 구성이 되어있습니다.
이말인 즉슨, 이 노드들이 연결된 형태의 자료구조를 바로 LinkedList라고 하는 것입니다.
예를 들어, 학교에서 어느 반의 모든 학생들의 데이터를 저장한다고 했을 때, 학생 한명 한명의 신상정보 자료를 노드로 만들고, 1번 학생의 신상정보 자료에 2번 신상정보 자료가 어디 있는 지 표시를 해 놓는 방식인 것입니다.
쉽게 말해서 줄줄이 소세지마냥 자료를 엮어 놓은 것이라고 생각하면 되겠습니다.

반면, 배열은 학생들의 데이터를 한 곳에 쭉 쌓아 올린 모양새라고 생각하면 됩니다.

그래서 전에 말했듯이 데이터를 추가하거나 삭제 할 때는 쌓아 올린 수가 많은만큼 어려운 것인데, 이 LinkedList는 엮여 져있는 pointer만 조금씩 수정해 주면 해당 과정이 쉽게 가능해져 시간 소모가 다른 것입니다.
노드 중에서는 고유한 노드가 존재하며 이 노드들은 다음과 같습니다.
Head: 가장 앞에 위치한 노드
- LinkedList의 값이 있더라도 Head 노드는 반드시 비어있습니다. 따라서 head 노드에는 무조건 null값을 주게 됩니다. 그래서 head node는 보통 dummy node라고 불리기도 합니다.(아무런 값이 존재하지 않고 그저 수단으로만 사용되기 때문)
Tail: 가장 뒤에 위치한 노드
- Tail은 자신의 다음에 가리킬 노드가 없기 때문에 Tail의 next pointer 또한 null입니다.
- 단순 연결 리스트에서는 노드가 뒤에 계속 추가 된다면 tail 노드는 바뀔 수 있지만, 이중 연결 리스트에서는 tail노드를 따로 지정을 해두기 때문에(이름이 '이중'인 이유) tail노드가 바뀌지 않습니다.
2. 검색
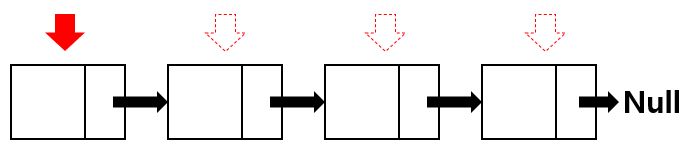
LinkedList에서의 검색은 ArrayList의 검색과 마찬가지로 head 노드에서부터 tail 노드까지 순차적으로 순회하면서 데이터를 찾아갑니다. 그렇기 때문에 마찬가지로 O(N)의 시간 복잡도를 가집니다.
ArrayList는 대신 index로 검색을 하는 경우 Randon Access(임의 접근 방식)가 가능하여 데이터를 처음부터 찾을 필요가 없기 때문에 O(1)의 시간 복잡도를 갖습니다.
3. 추가
'추가'는 원하는 노드를 하나 만들고 그 노드와 Tail노드의 next pointer를 연결하는 작업입니다.
마찬가지로 처음부터 끝까지 순회하면서 마지막 노드가 가리키고 있는 Null 위치에 우리가 원하고자 하는 노드를 추가 시키는 개념입니다.
ArrayList와는 달리, 끝 노드를 찾아야 하지 않아도 되고 그저 tail노드에서 새로운 노드를 추가하는 것이기 때문에 O(1)
의 시간 복잡도를 갖습니다.
4. 삽입
삽입은 제일 끝이 아니라 중간에 넣는 경우를 말하며 LinkedList는 ArrayList와는 다르게 데이터를 뒤로 한 칸씩 전부 밀어줄 필요가 없습니다. 그냥 간단히 pointer만 바꿔주면 되기 때문에 논리는 간단하지만 삽입 위치를 찾기 위해서는 순회를 통해 찾아야 하기 때문에 시간복잡도는 O(n) 입니다.
해당 과정은 다음과 같이 진행됩니다.
1. 먼저, 삽입을 원하는 노드를 생성한다.
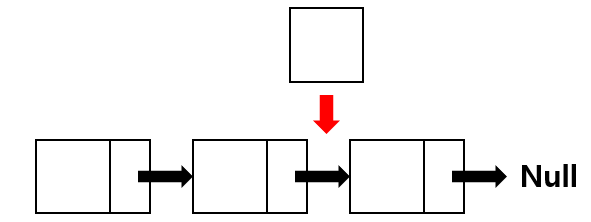
2. 해당 노드의 previous(이전의) node의 next 포인터를 본인 노드와 연결하고 previous node의 next pointer가 가리키고 있던 노드를 본인 노드의 next pointer로 가리킴로써 연결을 삽입을 마무리한다.
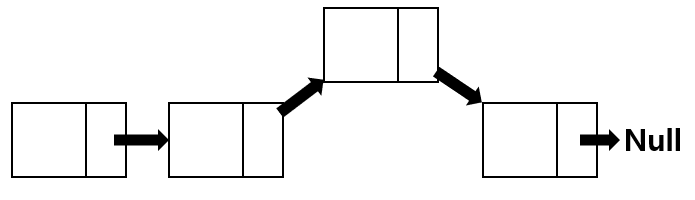
5. 삭제
LinkedList에서 삭제하고자 하는 노드가 있을 때는 그 위치를 찾아가야 하기 때문에 결정되는 시간복잡도는 O(N)입니다.
- head와 tail노드로 무작정 알아낼 수 없기 때문
ArrayList에서는 삭제할 위치를 찾고 뒤의 데이터들을 앞으로 한 칸씩 당기는데 또 시간이 O(N)만큼 소요가 됐다면,
LinkedList는 데이터를 당겨오지 않고 pointer만 조금 바꾸어 주면 삭제 과정이 자동으로 이루어지게 됩니다.
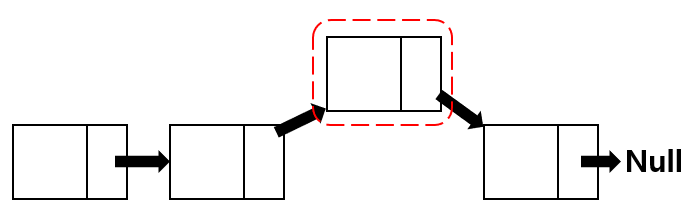
빨간 점선으로 된 노드를 삭제해야 한다고 합시다. 앞으로 삭제하고자 하는 노드를 삭제노드, 그 노드의 이전 노드는 이전노드 다음 노드는 다음노드라 부르겠습니다.
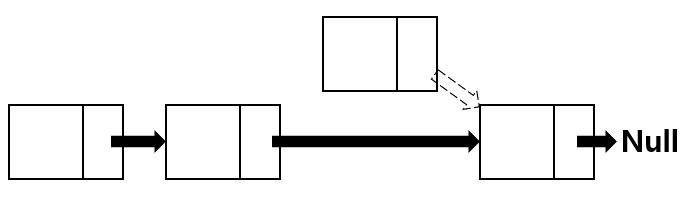
이전 노드의 next pointer는 삭제 노드의 next pointer가 가리키고 있던 노드를 가리키게되고 삭제 노드의 next pointer는 아무것도 가리키지 않는 상태인 null 상태가 되게 합니다.
즉, node.next = null; 로 표현할 수 있습니다.
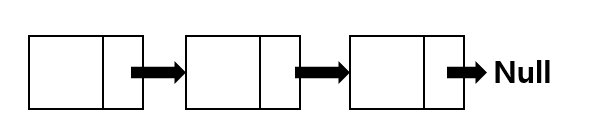
그 이후 자바에서는 garbage collector에 의해 붕떠 있던 삭제 노드는 알아서 사라지게 됩니다. 그리하여 LinkedList의 삭제를 진행한 후 연결이 잘 되어 있는 것을 볼 수 있습니다.
6. Linked List의 장단점
장점
- 배열의 복사나 재할당 없이 데이터 추가 가능 + 유연한 공간
- ArrayList는 배열이 꽉 차있는 경우 크기를 늘려 준 다음 데이터를 다시 추가해 주는 과정을 진행해야 했는데 LinkedList는 쓰는 공간만큼만 크기가 늘었다 줄었다 하기 때문에 메모리 측면에서 훨씬 효율적입니다.
단점
- 데이터 접근에 대한 시간이 늘어남
- 배열(Array List)과 달라, Random Access가 되지 않기 때문에 원하는 노드를 찾아야 하는 경우 O(N)의 시간복잡도가 발생한다는 점이 단점이라면 단점이겠습니다.
LinkedList vs. Array
| Linked List | Array List | |
| 추가 | O(1) | O(1), O(N) |
| 삽입 | O(N) | O(N) |
| 삭제 | O(N) | O(N) |
| 검색 | O(N) | O(1) |
위 표를 통해 LinkedList와 ArrayList의 장단점을 한번에 볼 수 있으며, 어느 상황에 어떤 자료구조를 사용해야 할 지를 생각해 보면 좋을 것 같습니다.
예를 들어, 리스트를 읽기만 할 때는 ArrayList가 압도적으로 좋지만 리스트의 추가, 삭제, 삽입을 한다면 LinkedList가 시간 복잡도 측면에서 더 좋은 경우가 있겠습니다.
7. LinkedList 구현
지난 시간 만들었던 IList 인터페이스를 구현 상속한 MyLinkedList 클래스를 구현해 보도록 하겠습니다.
package list;
public class MyLinkedList<T> implements IList<T> {
...
}
생성자
private int size;
private Node head;
public MyLinkedList() {
this.size = 0;
this.head = null; // dummy node
}먼저 MyLinkedList클래스의 멤버 변수로 크기를 나타내는 size변수와 head 노드를 선언합니다.
그리고 생성자에는 이 크기(size)와 헤드노드를 각각 0과 null로 초기화 시킵니다.
노드 클래스
private class Node {
T data;
Node next;
Node(T data) {
this.data = data;
}
Node(T data, Node next) {
this.data = data;
this.next = next;
}
}LinkedList는 노드 기반이기 때문에 사용할 노드 또한 만들어 줍니다.
앞서 말했듯, 노드에는 데이터를 담기 위한 data 변수와, 다음 node를 가리키기 위한 pointer 객체(next)가 필요한데요,
구현을 더 편하게 하기 위해서 노드의 생성자를 만들어주었는데 인자를 data 하나만 받는 경우와 data와 next pointer객체 두 가지를 받는 경우를 나누어 각각 경우에 맞게 초기화 시키는 생성자들을 만들어 주었습니다.
add
@Override
public void add(T t) {
Node curr = this.head;
while(curr != null) {
curr = curr.next;
}
Node node = new Node(t);
curr.next = node;
this.size++;
}curr이라는 노드는 순회를 위해서 현재 위치를 특정짓기 위한 노드이다. head 노드부터 시작해야 되기 때문에 head 노드를 curr노드에 대입합니다. (curr 노드 진입)
순회는 null이전까지 해야 하기 때문에 while 문에 조건을 붙여 반복해 주었습니다. curr의 next pointer를 curr로 지정하면서 계속해서 앞쪽으로 쭉쭉 순회가 되는 개념입니다.
반복문을 빠져나왔을 때는 LinkedList의 끝까지 왔을때이므로 추가하고자 하는 'node'를 새로 만들고 curr의 next pointer가 이 노드를 가리키게 하며 size는 1만큼 증가시킵니다.
insert
@Override
public void insert(int index, T t);{
if(index > this.size || index <0){
throw new IndexOutOfBoundsException();
}
Node prev = this.head;
Node curr = prev.next;
int i = 0;
while(i++ < index) {
prev = prev.next;
curr = curr.next;
}
Node node = new Node(t, curr);
prev.next = node;
this.size++;
}insert는 구현방식이 ArrayList와 크게 다르지 않다. 다만, ArrayList와 같이 뒤의 데이터를 전부 밀지 않고 pointer 몇 개만 조금 바꾸어 주면 됩니다.
먼저, 가장 처음의 상태는 prev 노드는 head노드이고, 그렇기 때문에 curr노드는 prev노드의 next pointer가 가리키는 노드여야 합니다. 즉, head 노드의 next pointer가 가리키고 있는 것은 null이므로 null을 가리키고 있는 것과 같은 상황입니다.
삽입하고자 하는 index의 수만큼 순회를 진행할 것인데, 반복문이 진행됨에 따라 prev노드와 curr노드를 다음 노드로 계속해서 이동해 주었고 해당 index만큼 반복이 진행 되었을 때는 prev노드와 curr노드에는 삽입을 원하는 위치의 노드로 초기화가 진행되어 있을 것입니다.
그 이후 삽입하고자 하는 node를 생성하되 인자로 curr노드를 넘겨 node 노드가 생성될 때 이 노드의 next pointer가 가리키는 노드는 curr 노드가 되도록 해줍니다.
- 생성한 노드: 데이터 field에는 t를 가지며 next pointer로 curr 노드를 가리키고 있는 노드
그리고 prev의 next pointer를 생성한 node로 해서 연결을 마무리 짓습니다. 마지막으로 삽입을 진행하였으니 배열의 크기를 1만큼 증가 시켜 줍니다.
clear
@Override
public void clear() {
this.size = 0;
this.head.next = null;
}ArrayList와 다르게 LinkedList 의 clear에서는 size를 0으로 초기화 시켜주는 것 뿐 아니라 LinkedList의 모든 연결을 끊어 주어야 하는데 head노드의 next pointer가 가리키고 있는 객체를 null로 초기화를 시켜주면 LinkedList의 clear 과정이 진행된다. (생각보다 간단하죠?)
- LinkedList를 타고 들어가는 방법은 오직 head노드를 통한 경로 밖에 없기 때문에 head노드와 다른 노드의 연결을 끊어주는 행위, 즉 null로 초기화 시키는 과정을 진행하면 자연스레 연결리스트의 초기화가 되는 것입니다.
delete
@Override
public boolean delete(T t) {
Node prev = this.head;
Node curr = prev.next;
while(curr != null) {
if(curr.data.equals(t)) {
prev.next = curr.next;
curr.next = null;
this.size--;
return true;
}
prev = prev.next;
curr = curr.next;
}
return false;
}LinkedList에서의 삭제는 마찬가지로 뒤의 데이터를 당겨주는 과정(시간 복잡도: O(N)소모)없이 포인터 몇 개만 조금 바꾸어 주는 것으로 구현할 수 있습니다.
먼저 기본 세팅은 앞선 기능들과 동일합니다.
while문을 통해 노드를 순회하고 조건문을 통해 조건에 맞는 prev노드와 curr노드가 정해졌을 때 curr노드는 삭제하고자 하는 노드이고 prev노드는 삭제하고자 하는 노드의 이전노드 일 것입니다.
prev 노드의 next pointer는 가리키고 있는 것은 삭제하고자 하는 curr 노드이기 때문에 이를 curr노드의 next pointer가 가리키고 있던 노드와 연결시킵니다.
그러고 나서는 curr의 next pointer는 아무것도 가리키지 않는 상태로 만들어 주기 위하여 null 값으로 초기화시켜 줍니다..
항상 마무리는 리스트의 크기 조정으로 마무리합니다. (this.size-- : 크기 1 감소)
deleteByindex
@Override
public boolean deleteByindex(int index){
if(index >= this.size || index < 0){
throw new IndexOutOfBoundsException();
}
Node prev = this.head;
Node curr = prev.next;
int i = 0;
while(i++ < index) {
prev = prev.next;
curr = curr.next;
}
prev.next = curr.next;
curr.next = null;
this.size--;
return true;
}deleteByindex는 index로 노드를 찾아 해당 노드를 삭제시키는 것이기 때문에 인자로 받는 index의 범위가 음수이거나 리스트의 size보다 크거나 같은 경우 false를 리턴할 수도 있겠지만 오류의 내용을 더 명확히 명시하기 위하여 IndexOutOfBound 예외를 throw 하게끔 하였습니다.
deleteByindex 또한 다른 것들과 마찬가지로 prev 노드와 curr노드를 초기화시키고 while 반복문을 index 까지 i를 증가시키면서 진행하고 그 안의 내용으로는 prev 노드와 curr 노드를 다음 노드로 이동하는 과정을 진행합니다.
반복문이 종료된 시점에는 curr노드는 index만큼의 노드가 되고 prev 노드는 그 이전의 노드가 되기 때문에 위의 delete에서 했던 것과 동일한 방법으로 삭제시킵니다.
get
@Override
public T get(int index){
if (index >= this.size || index < 0) {
throw new IndexOuOfBoundException();
}
Node curr = this.head.next;
int i = 0;
while(i++ < index) {
curr = curr.next;
}
return curr.data;
}get은 원하는 노드의 data만 얻고 싶은 것이기 때문에 prev노드를 사용하지 않아도 됩니다.(only data!)
내용은 똑같이 curr 노드를 생성하여 이를 원하는 index까지 이동시켜 그 노드의 data를 리턴하는 식입니다.
- 위 코드에서 curr 노드에 head 노드를 대입시키는 것이 아니라 head 노드의 next pointer가 가리키는 노드를 대입시킨 이유는 head 노드에는 어차피 데이터(값)가 존재하지 않기 때문입니다.
indexOf
@Override
public boolean indexOf(T t) {
Node curr = this.head.next;
int index = 0;
while (curr != null) {
if(t.equals(curr.data)) {
return index;
}
curr = curr.next;
index++;
}
return -1;
}indexOf 메소드는 인자로 받아온 t와 일치하는 노드의 index를 반환하는 메소드입니다.
- 데이터의 index를 리턴하는 메소드
curr 노드를 생성하고 while 반복문을 통해 index를 0부터 증가시키면서 리스트의 끝까지 반복시키고 curr 노드를 이동시켜 리스트를 순회합니다. 그리고 현재 노드와 인자 t가 일치할 때, 그때의 index를 반환하면 됩니다.
isEmpty
@Override
public boolean isEmpty() {
return this.head.next == null;
}ArrayList에서 했던 것처럼 size가 0인 것으로 isEmpty 메소드를 구현해도 되지만 LinkedList스럽게(?) 구현하려면 head 노드의 next pointer가 가리키고 있는 노드가 null이면 연결리스트의 초기 상태, 즉 리스트가 비어있는 것이기 때문에 이 logic을 리턴합니다.
contains
@Override
public boolean contains(T t) {
Node curr = this.head.next;
while(curr != null) {
if(t.equals(curr.data)) {
return true;
}
curr = curr.next;
}
return false;
}contains 메소드 역시 ArrayList와 마찬가지로 반복문을 통해 하나씩 돌면서 equals 메소드로 리스트의 원소와 일치하면 true(=1) 아니면 false(=0)을 반환해 주는 알고리즘입니다.
- 이 역시도 노드끼리의 연결을 바꿀 필요가 없기 때문에 prev 노드를 지정해 주지 않고 구현합니다.
size
@Override
public int size() {
return this.size;
}리스트의 크기를 반환하는 메소드는 사실 반복문을 돌면서 tail 노드까지 접근하면서 index를 증가시키는 방법도 있지만 그렇게 되면 시간복잡도 O(N)이 발생하므로 비효율적입니다.
따라서 그냥 'simple is the best' 란 말처럼 this.size를 반환합니다.
8. 자료구조 시간 복잡도 비교
- 평균 시간 복잡도(Average)
| 자료구조 | Access | Search | Insertion | Deletion |
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Singly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Doubly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Hash Table | Θ(1) | Θ(1) | Θ(1) | Θ(1) |
| Binary Search Tree | Θ(log2n) | Θ(log2n) | Θ(log2n) | Θ(log2n) |
| AVL Tree | Θ(log2n) | Θ(log2n) | Θ(log2n) | Θ(log2n) |
| B Tree | Θ(log2n) | Θ(log2n) | Θ(log2n) | Θ(log2n) |
- 최악의 경우 시간 복잡도(Worst)
| 자료구조 | Access | Search | Insertion | Deletion |
| Array | O(1) | O(n) | O(n) | O(n) |
| Stack | O(n) | O(n) | O(1) | O(1) |
| Queue | O(n) | O(n) | O(1) | O(1) |
| Singly Linked List | O(n) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(n) | O(1) | O(1) |
| Hash Table | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log2n) | O(log2n) | O(log2n) | O(log2n) |
| AVL Tree | O(n) | O(n) | O(n) | O(n) |
| B Tree | O(log2n) | O(log2n) | O(log2n) | O(log2n) |
'CS 지식 > 자료구조와 알고리즘(Java)' 카테고리의 다른 글
| [자료구조 | Java] Stack(스택) (0) | 2022.12.28 |
|---|---|
| [자료구조 | Java] Double LinkedList(이중 연결 리스트) (0) | 2022.12.27 |
| [자료구조 | Java] 리스트(List) - ArrayList (0) | 2022.12.27 |
| [자료구조 | Java] 자료구조와 알고리즘 기초 (0) | 2022.12.27 |
| [자료구조&알고리즘 with Java] 자료구조 및 알고리즘 시작 (0) | 2022.12.26 |
소중한 공감 감사합니다