[자료구조와 알고리즘 | 파이썬] Shortest Path Algorithms(최단 거리 알고리즘) & Dijkstra Algorithm(다익스트라 알고리즘) & Bellman-Ford Algorithm(벨만-포드 알고리즘) + 위상 정렬(Topology sort)
2022.12.31- -
1. Shortest Path Algorithms (최단거리 알고리즘)
1-1. Single-Source Shortest Paths
최단 거리 문제에서, 우리는 weight(가중치)가 부여된 방향 그래프(directed graph) G = (V, E)가 주어집니다.
(앞으로 나오는 G=(V, E) 에서 대문자 V와 대문자 E는 각각 노드(vertex)와 간선(edge)의 집합을 의미합니다.)
가중치 함수(weight function)는 아래 식과 같습니다.

위 식의 의미는 edge를 real-valued weights(실수 가중치)에 매핑하겠다는 의미입니다.즉, 각 edge마다 주어지는 path에 대한 값이 존재한다는 것인데요.
특정 path의 weight를 의미하는 w(p) (p = <v0, v1, ..., vk>인 곳에서)는 해당 path를 구성하는 edge들의 총 weight 합을 나타냅니다.
따라서 path를 지나면서 각 노드 마다 weight가 점점 쌓이게 되는 구조입니다.

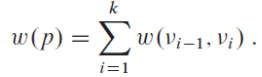
우리는 이때, 최단 경로의 가중치를 아래와 같은 델타로 정의합니다.

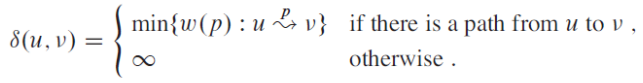
vertex u에서 vertex v까지의 최단 경로는 가중치가 있는 임의의 경로(path) p로 정의됩니다.
1-2. Optimal substructure of a shortest path (최단 경로의 최적 구조)
최단 경로 알고리즘은 일반적으로 두 정점 사이의 최단 경로가 그 안에 다른 최단 경로를 포함한다는 속성을 따릅니다.
최적의 하위 구조(optimal substructure)는 동적 프로그래밍과 그리디 알고리즘에도 적용될 수 있었던 지표 중 하나임을 반드시 기억하셔야 합니다.
즉, 최단 경로(shortest path)는 그 안에 존재하는 하위 경로(sub path)에서도 최단 경로가 계속해서 유지되는 구조입니다.

Lemma. "최단 경로의 하위 경로는 최단 경로다.
주어진 가중, 방향 그래프에서 가중치 함수 w에 대해 p가 vo에서 vk까지의 최단 경로가 되도록 하려면,
0 < i < j < k를 만족하는 어떠한 i와 j에 대해서 vi에서 vj로 가는 p의 subpath가 되도록 하고, 그때 pij역시 vi에서 vj까지 가는 최단 경로입니다.
1-3. Negative-weight edges (음수 가중치 간선)
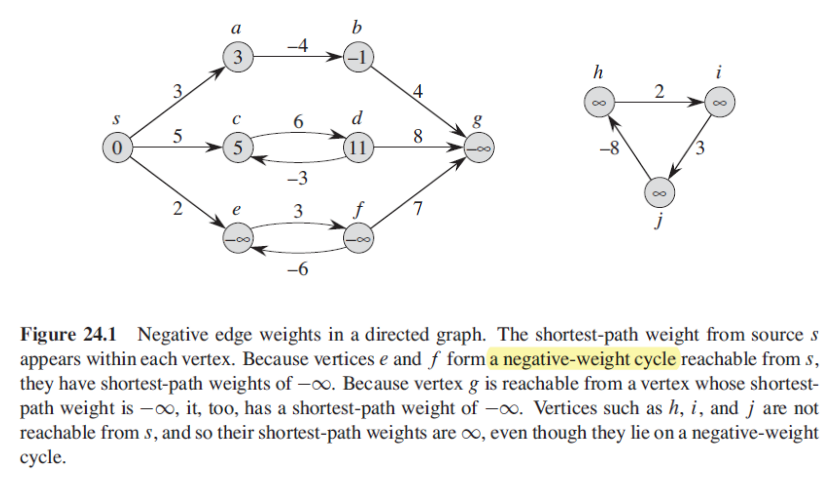
위 그림은 방향 그래프에서 edge가 음수 가중치를 갖는 그래프입니다. source s로부터 특정 vertex까지의 최단 경로 가중치의 값은 각 vertex 내부에 적혀있습니다.
e 노드와 f 노드가 source s로부터 음수 가중치 사이클(negative-weight cycle)을 형성하였기 때문에, 두 노드는 최단 경로 가중치로 음의 무한대 값을 갖게 됩니다.
g 노드는 최단 경로가 음의 무한대인 노드로부터 도달 가능하기 때문에 이 노드 역시 자동으로 음의 무한대 가중치가 최단 경로가 됩니다.
h나 i, j와 같은 노드들은 s로부터 도달할 수 없기 때문에 그 노드들이 비록 음수 가중치 사이클에 놓여있다고 하더라도 그들의 최단 경로는 무한대로 설정됩니다.
- c ↔ d 는 cycle인데 한 번 갔다가 다시 오면 cost 3이 든다.(즉, 한 cycle에 cost 3 발생)
- e ↔ f 도 cycle이지만 한 번 갔다가 다시 오면 cost -3이 된다. (즉, 한 cycle에 cost -3 발생) -> negative-weight cycle
- 그런데 이 negative-weight cycle이 있으면 shortest path가 존재할 수 없는데,
그 이유는 shortest path는 최소한의 cost가 드는 거리를 찾는 것인데 negative cycle을 발견하게 되면 그 부분에서는cost를 계속해서 줄이려는 방향으로 진행이 될 것이므로 그 loop를 빠져나가는 경우가 생기지 않아 shortest path는 결국 negative infinity가 된다. - s에서 시작해서 h, i, j 까지 갈 수있는 연결된 edge가 없기 때문에 해당 노드들은 무한대의 값을 가지게 된다.
- 이 노드들에게 가려면 무한대의 path를 가도 갈 수 없지만 가장 최대의 값인 무한대로 설정한 것
1-4. Representing shortest paths (최단거리 표현 방식)
주어진 그래프 G = (V, E)에서 각각의 vertex v ∈ V 에 대해 우리는 또 다른 vertex인 predecessor(선임, 이전의)를 의미하는 v.π 를 갖습니다.
그래서 v.π는 v 노드까지 왔을 때, 바로 앞 노드를 가리키고
- (아래 예제에서) t.π = s
각 vertex에서는 계속해서 이러한 predecessor를 관리해 주어야 합니다.
- predecessor는 경로마다 다른 값을 가질 수 있습니다.
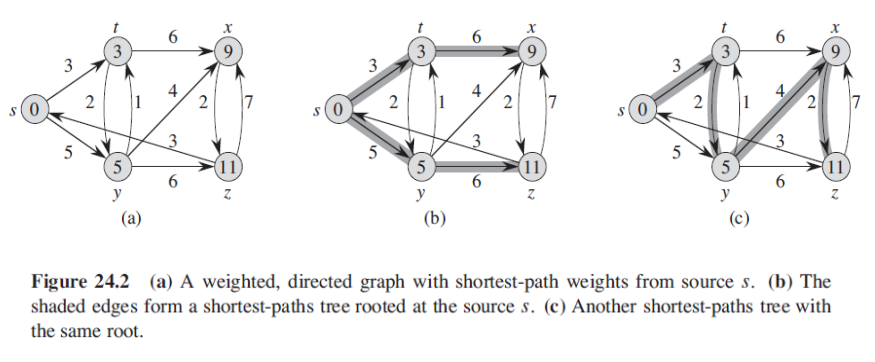
(a)에 대한 shortest path를 구해 보면 (b)처럼 될 수도 (c)처럼 될 수도 있습니다.
- (a): source s로부터 최단 경로 가중치를 지닌 가중치, 방향 그래프
- (b): 그림자(음영)가 진 edges는 source s를 root로 하는 최단 경로 트리(shortest-path tree)를 형성한다.
- (c): 같은 root에 대한 또 다른 최단 경로 트리(shortest-path tree)
그래서 만약 t 노드에 올 때 바로 전에 어떤 노드를 거쳤는지 기록하는 경우에 이를 t.π 와 같이 기록할 수 있습니다.
1-5. Initialize-Single-Source
각 노드 v ∈ V 에 대해 source에서 특정 v 노드로 가는 최단 경로의 가중치에 대한 upper bound(상한선)을 유지하는 v.d 속성을 갖습니다.
v.d를 최단 경로의 추정치(estimate)이라고 부르고, 아래 식을 통해 이러한 최단 경로 추정치와 이전 경로를 initialize 시킬 수 있습니다.
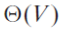
Time procedure: <pseudo code>
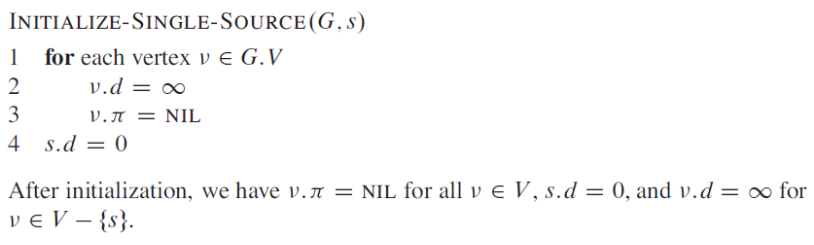
- G는 내가가지고 있는 graph를 의미.
- s는 source(시작) 노드.
- V는 vertex의 집합.
- v.d 는 shortest-path의 estimate
- 여기서 추정치라 함은, source에서 모든 vertex까지의 계산된 shortest distance 값이므로 처음에는 모두 무한대(∞)로 초기화한다.
- 처음에는 그 값이 어떻든 무조건 초기화 시켜줘야 하기 때문이기도 하고 해당 노드까지 갈 방법이 아직까지 없다는 의미로 그렇게 설정을 한다.
- 그 바로 앞에 있는 노드(v.π)도 처음이기 때문에 값을 아직 받은 것이 없어 None으로 초기화 한다.
- s.d 즉, source에서 source까지의 distance는 당연히 0이다.(같은 노드이니까)
- 여기서 추정치라 함은, source에서 모든 vertex까지의 계산된 shortest distance 값이므로 처음에는 모두 무한대(∞)로 초기화한다.
1-6. Relaxation
relaxation이란 shortest path를 찾기 위해서 공통적으로 사용하는 방법입니다. 단어 뜻 "완화"에서 알 수 있듯이 통통 높이 뛰어 있던 값들을 계산에 따라 나오는 더 작은 값들로 안정시키는 작업을 생각하면 됩니다.
edge(u, v), 즉 u에서 v로 가는 간선을 relaxing 하는 과정은 u를 통해 지금까지 발견된 v에 대한 최단 경로를 갱신시킬 수 있는지 테스트하고, 만약 갱신시킬 수 있다면 v.d 와 v.π를 업데이트 하는 것으로 구성됩니다.
relaxing 단계는 최단 경로 추정치인 v.d의 값을 감소시키고 v의 이전 속성 v.d를 업데이트할 수 있습니다.
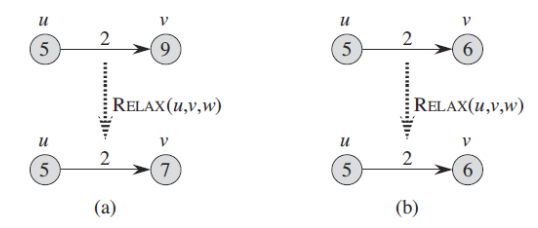
위 그림은 w(u, v) = 2인 (u, v)의 edge를 relaxing하는 과정을 나타낸 것입니다. 각 vertex의 최단 거리 추정치는 vertex 안에 표기됩니다.
(a) 그림에서 relaxation에 앞서 v.d > u.d + w(u, v)이기 때문에 v.d 값을 감소시킵니다.
- v.d = 9
- u.d + w(u, v) = 5 + 2 = 7
(b) 그림에서는 (u,v) edge가 relaxing 되기 전에 v.d <= u.d + w(u, v)이고 그래서 relaxation 단계에서 v.d 값을 바꾸지 않은채로 냅두게 됩니다.
- v.d = 6
- u.d + w(u, v) = 5 + 2 = 7
정리하자면 아래와 같습니다.
- 현재까지 알려진 u까지의 거리 - u.d
- 현재까지 알려진 v까지의 거리 - v.d
- relax한다는 것은 v.d 를 더 낮은 값으로 update 한다는 것입니다.
- 현재 v의 경로보다 u를 들리는 경우에 더 작은 가중치로 갈 수 있는지를 확인하고, 더 짧다면 그 경로로 update 합니다.
1-7. pseudo code
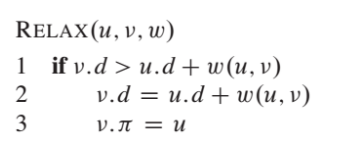
이번 챕터의 각 알고리즘은 initialize-single-source를 호출한 다음, edge를 반복적으로 relax시킵니다.
또한, relaxation은 최단 경로 추정치와 이전 추정치를 변경하는 유일한 수단입니다.
또한 이 챕터의 알고리즘은 각 edge를 relax 시키는 횟수와 edge를 relax 시키는 순서에 따라 달라집니다.
Dijkstra's algorithm(다익스트라 알고리즘)과 방향 비순환 그래프(directed acyclic graph)에 대한 최단 경로 알고리즘은 각 edge를 정확히 한번만 relax 합니다.
- 즉, 노드 당 딱 한 번
※ Bellman-Ford(벨만-포드) 알고리즘은 각 edge를 |V| - 1회 relax 합니다
2. The Bellman-Ford algorithm
벨만-포드 알고리즘은 edge의 weight가 음수인 일반적인 경우에 single-source shortest-paths(단일 소스 최단 경로) 문제를 풀어냅니다.
주어진 weights에서, source s와 weight function w: E -> R 일 때, 방향 그래프 G = (V, E)에서 Bellman-Ford 알고리즘은 source로부터 도달할 수 있는 음수 가중치 cycle이 존재하는지 아닌지를 가리키는 boolean value(True or False)를 반환합니다.
만약 그러한 cycle이 존재한다면, 알고리즘은 어떠한 solution도 존재하지 않는다고 표시합니다.
만약 그러한 cycle이 없다면, 그 알고리즘은 최단 경로와 그 경로마다의 가중치를 만들어냅니다.
Bellman-Ford의 장점은 edge의 weight가 negative여도 동작한다는 것입니다.
- 다익스트라는 동작 안 함. (다익스트라는 뒤에서 나옵니다.)
그렇기 때문에 가장 먼저 negative cycle이 있는지를 판단해야 합니다.
- 만약 있다면 algorithm을 돌려도 solution이 구해지지 않는다.
- 없으면 그냥 shortest path를 구한다.
따라서 그래프가 방향 그래프이면서 음수 가중치(negative weights)가 존재한다면 벨만-포드 알고리즘을 사용합니다.
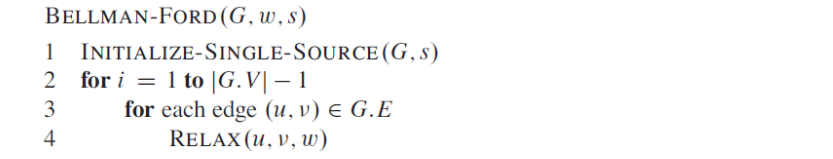
1번 라인에서 모든 vertex들의 d값과 π값을 초기화 시킵니다. 이 알고리즘은 그래프의 edge를 |V| - 1 회 통과시킵니다.
각각의 pass에서는 2-4번 라인의 for-loop에서 한번의 순회, 그리고 그래프의 edge를 한 번 relaxing시키는 것으로 구성됩니다.
- Initialize
- for문 - {|G.V| - 1 }번
- |G.V| -> vertex의 갯수
- for 문 - Edge의 집합에 속하는 모든 edge를 한 번씩 돌면서 relaxing 시킨다.
- 모든 edge를 update
이 결과 negative (weight) cycle이 있다면 이상한 결과가 들어가 있을 것이고 그렇지 않으면 shortest path가 구해져 있게 됩니다.

그래프 G = (V, E)가 source s와 weight function w: E -> R인 가중치, 방향 그래프라고 하고, G는 s로부터 도달가능한 어떠한 음수 가중치(negative weight) cycles이 존재하지 않는다고 가정합시다.
그러면 위 psuedo 코드 BELLMAN-FORD에서 2-4번 라인 for-loop의 {|V| - 1}번 만큼 순회를 거쳐서 우리는 s로부터 도달 가능한 모든 vertices v에 대한 v.d = δ(s, v)를 얻어냅니다.
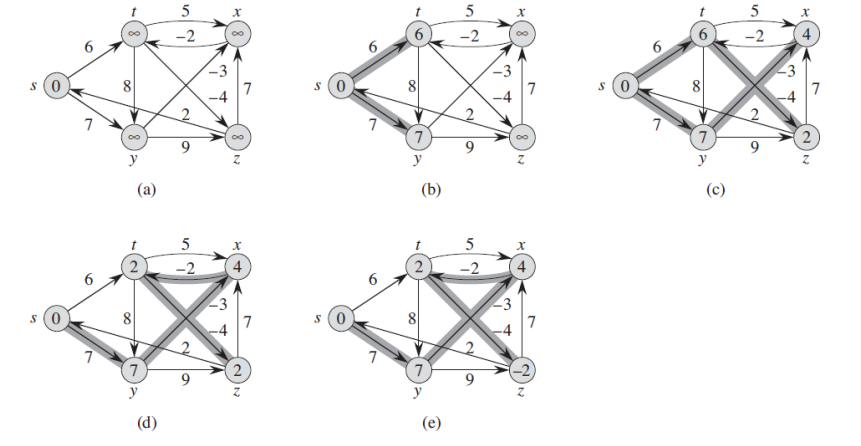
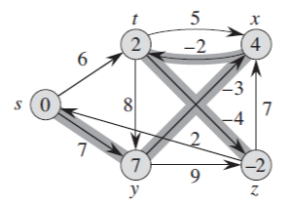
위 과정은 벨만-포드 알고리즘의 실행 모습입니다. source vertex는 s입니다.
d 값은 각 vertex 안에 적혀있고 그림자가 진 edge들은 predecessor value를 나타냅니다.:
- 만약 edge (u, v)가 그림자가 졌다면 v.π = u 임.
이러한 예제에서 각 pass는 (t, x), (t, y), (t, z), (x, t), (y, x), (y, z), (z, x), (z, s), (s, t), (s, y)의 순서로 edge들을 relax합니다.
- (a): 첫 번째 pass에서 edges를 지나기 바로 전 상황
- (b)-(e): 연속적인 pass에서 edges를 지나고 나서의 상황
초기에는 모든 노드에 무한대값이 들어있기 때문에 s에서 시작하는 path 값들로만 update 될 것입니다.
각 edge를 어떤 순서대로 relax 하는 지는 중요하지 않습니다.
다만 기억해야 할 점은 결과적으로 source에서 dest 노드까지 가면서 거치는 노드들에 대한 각각의 shortest path 정보
(v.d, v.π)를 모든 노드들이 각자 다 갖고 있게 될 것이라는 것입니다.

|V| - 1회의 pass를 거친 후, 5-8번 라인에서 negative-weight cycle에 대한 체크를 하고 그에 맞는 boolean 값을 return 합니다.
벨만 포드 알고리즘은 2-4번 라인에서 |V| - 1회 pass를 거친 edge들 각각에 대해 1번 라인에서 초기화되는 과정이 O(V)만큼의 시간이 소요되고 5-7번 라인의 for문에서 O(E)만큼의 시간이 소요되기 때문에 총 O(VE) 시간복잡도로 실행됩니다.
- O(E(V-1)) => O(EV)
앞서 |V|-1 만큼 for loop를 돌려서 얻어낸 결과가 shortest path인지 아니면 strange value인지를 알아내는 작업이 필요한데 이는 위의 코드 5-8번 라인과 같이 작성하면 됩니다.
만약 모든 edge에 대해서 반복하였는데도 불구하고 v.d > u.d + w(u, v) 인 경우가 또 발생하면, 즉 u를 통해서 더 빨리 갈 수 있는 경우가 어떤 edge에서 여전히 존재한다고 판단 되었을 경우는 bellman-Ford 알고리즘이 제대로 작동하지 않았다는 것을 의미하기 때문에 이 경우는 negative cycle이 있다고 유추할 수 있는 것입니다.
- 그게 아니라면 결과값이 제대로 구해진 것이기 때문에 True를 리턴
2-1. 코드로 구현
def bellman_ford(graph, source):
# intialize
distance = {} # v.d
predecessor = {} # v.π
for node in graph.keys():
distance[node] = float('inf')
predecessor[node] = None
distance[source] = 0
# relax all edges for V-1 times
for _ in range(len(graph) - 1): # |V| - 1
for u in graph: # 이중 dictionary 일 것이기 때문에 u도 dictionary임 -> key를 하나씩
# w is the weight of edge (u, v)
for v, w in graph[u].items():
if distance[v] > distance[u] + w:
distance[v] = distance[u] + w
predecessor[v] = u
# check for a negative-weight cycle
for u in graph:
for v, w in graph[u].items():
if distance[v] > distance[u] + w:
return False, distance, predecessor
return True, distance, predecessor
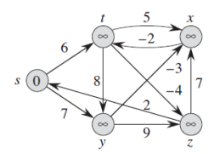
Fig24_4 = { # 앞에 있는 그래프 그림에 대한 adjacency list
's': {'t': 6, 'y': 7},
't': {'x': 5, 'y': 8, 'z': -4},
'x': {'t': -2},
'y': {'x': -3, 'z': 9},
'z': {'s': 2, 'x': 7}
}
check, dist, pre = bellman_ford(Fig24_4, 's') # 35; graph와 source 노드를 넘겨줌
if check:
print(pre)
print(dist)
- graph의 key는 u -> predecessor
- v는 현재 노드
- 처음에 distance[v]가 무한대일 것이기 때문에 distance[u] + w(eight) 보다는 무조건 클 것이고 해당 노드의 distance[v]를 distance[u] + w로 초기화하는 것이다.
- 그리고 해당 노드의 predecessor를 u로 update한다.
- predecessor 는 shortest path가 정해지면 해당 노드에 오기까지 바로 전 노드를 의미한다.
def bellamn_ford(grpah, source):
# intialize
distance = {} # v.d
predecessor = {} # v.ㅠ
for node i in graph.keys():
predecessor[node] = None
distance[source] = 0
for문을 한 번씩 돌 때마다 distance가 어떻게 초기화 되는지 한 번 찍어보면 아래와 같게 나옵니다.
{'s': inf}
{'s': None}
{'s': inf, 't': inf}
{'s': None, 't': None}
{'s': inf, 't': inf, 'x': inf}
{'s': None, 't': None, 'x': None}
{'s': inf, 't': inf, 'x': inf, 'y': inf}
{'s': None, 't': None, 'x': None, 'y': None}
{'s': inf, 't': inf, 'x': inf, 'y': inf, 'z': inf}
{'s': None, 't': None, 'x': None, 'y': None, 'z': None}
2-3. Detecting Negative-Weight Cycles in a Disconnected Graph
연결이 끊어진 그래프(Disconnected Graph)에서 negative-weight cycles를 찾는 법
연결이 끊어진 그래프에서 negative-weight cycles을 찾기 어려운 이유는 다음과 같습니다.

- 처음에는 모든 노드를 초기화하는 과정을 진행합니다.
- source에서 c까지의 distance -> 무한대
- s에서 e, f까지의 distance -> 무한대
- bellman-ford 알고리즘을 수행합니다.
- 총 노드 4개 -> |V| - 1 -> for loop 3번
- 각 노드별로 모든 edge들에 대해서 relaxing 진행 (s제외 모든 노드 무한대)
- 초반에 비교 대상은 무한대보다는 무조건 더 짧은 경로입니다.
- c = 5로 update
- e 혹은 f로 오는 경로는 없기 때문에 여전히 무한대로 둡니다.
- 초반에 비교 대상은 무한대보다는 무조건 더 짧은 경로입니다.
- 각 노드별로 모든 edge들에 대해서 relaxing 진행 (s제외 모든 노드 무한대)
- 총 노드 4개 -> |V| - 1 -> for loop 3번
- 현재 얻은 distance가 shortest distance인지를 판단합니다.
- c.d = 5 -> shortest distance
- e.d, f.d 모두 더 짧은 경로가 존재하지 않기 때문에 negative cycle가 위 그림에는 없습니다.
- True 리턴 : 내가 가진 그래프에 negative cycle가 없음을 의미합니다.
- 그런데 e와 f는 실제로 negative weight cycle을 형성하고 있습니다.
이러한 경우에 negative cycle을 찾아내기 위해서는 어떻게 해야 할까요?
solution -> 각 vertex의 distance를 100으로 초기화한다.(꼭 100이 아니어도 그냥 적당한 값으로 초기화)
{'s': None, 'c': 's', 'e': None, 'f': None}
{'s': 0, 'c': 5, 'e': inf, 'f': inf}{'s': None, 'c': 's', 'e': 'f', 'f': 'e'}
{'s': 0, 'c': 5, 'e': 88, 'f': 94}
무한대의 값에서 100으로 바꾸면 False를 반환하게 되므로 아무 값도 나오지 않게 됩니다.
- vertex를 모두 100으로 초기화
- c를 먼저 relax 하면 5로 update
- e를 relax하면 f를 통해 오는 경우 94 만에 올 수 있기 때문에 update(94 < 100)
- e가 방금 94로 update 되었기 때문에 f는 e를 통하면 97 만에 올 수 있음.
- c는 그대로이고, e는 계속해서 내려갈 것임(계속 더 작은 값이 존재하기 때문에)
- 이에 따라 f도 계속해서 shortest가 계속 update 됨
그러면 결과적으로 c는 아무리 for문을 돌려도 그대로 일 것이지만, e는 for문을 돌릴 수록 더 작은 shortest distance가 존재하기 때문에 모든 vertex에 대해 for문이 종료되면 결과적으로 False가 리턴 될 것이고 이를 통해 궁극적으로 negative cycle을 detect 할 수 있게 되는 것입니다.
이를 통해 무조건 inf로 초기화하는 것보다 충분히 큰 값으로 초기화 시키야 negative cycle을 찾을 수 있게 되는 경우가 있는 것입니다.
이때 그 충분히 큰 값이란, 아래 공식으로 도출해 낼 수 있습니다.
- edge의 갯수 x weight 의 최댓값
2-4. 벨만 포드 알고리즘과 관련된 문제
1865번: 웜홀
첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500),
www.acmicpc.net


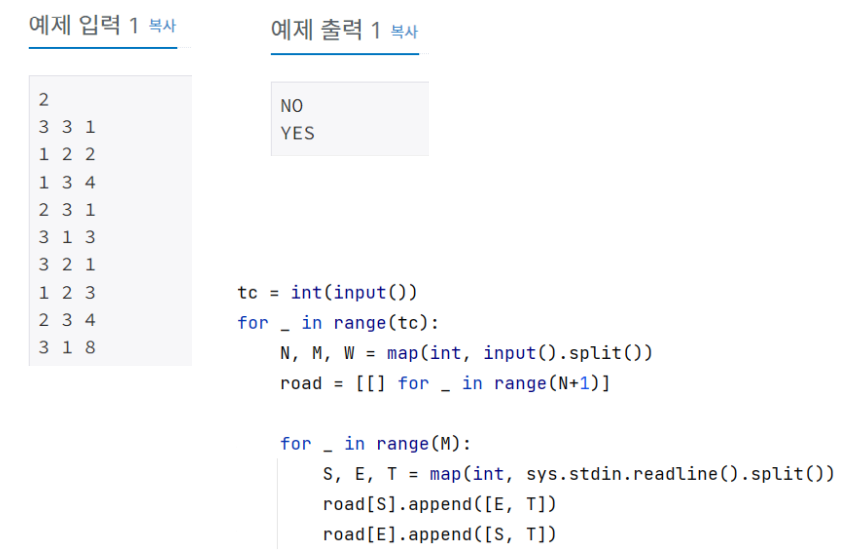

N: vertex의 갯수
M: edge의 갯수
W: negative edge의 갯수
S와 E가 undirected로 이어졌습니다.
M+2 번째 줄 부터는 웜홀이므로 S가 시작, E가 도착이 되며, T는 negative edge입니다.
import sys
def bellman_ford(start):
dist[start] = 0
for i in range(1, N+1):
for s in range(1, N+1):
for next, time in road[s]:
if dist[next] > dist[s] + time:
dist[next] = dist[s] + time
if i == N:
return True
return False
sys.stdin = open('bj1865_in.txt', 'r')
input = sys.stdin.readline
tc = int(input())
for _ in range(tc):
N, M, W = map(int, input().split())
road = [[] for _ in range(N + 1)]
dist = [M * 10] * (N + 1)
for _ in range(M):
S, E, T = map(int, sys.stdin.readline().split())
road[S].append([E, T])
road[E].append([S, T])
for _ in range(W):
S, E, T = map(int, sys.stdin.readline().split())
road[S].append([E, -T])
if bellman_ford(1):
print("YES")
else:
print("NO")NO
YES
위 코드를 보면 그래프를 저장할 때 인접리스트 방식으로 저장했는데 자료구조를 dictionary로 하면 안되는 이유는 무엇일까요?
지난 포스팅 그래프에서 설명했지만 key값이 string이 아닌 경우, 즉 key값이 int 형의 정수라면 리스트로 저장하여 푸는 것이 더 편합니다.
이차원 리스트로 저장하는 경우에 크기를 (vertex 갯수 + 1)만큼 초기화합니다.
- 0번 인덱스는 비워두기 위함.
초기 distance를 초기화할 때 값을 무한대로 하지 않고 충분히 큰 값으로 설정합니다.
- edge의 갯수 x weight 의 최댓값
3. Dijkstra's algorithm (다익스트라 알고리즘)
다익스트라 알고리즘은 모든 가중치가 음수가 아닌 경우에 가중치, 방향 그래프(weight dirtected graph) G에서 단일 소스 최단 경로(single-source shortest-paths) 문제를 해결합니다.
따라서 이번 섹션에서 각 edge (u, v)에 대해 w(u, v) >= 0 임을 가정합니다.
뒤에서 나오겠지만, 다익스트라 알고리즘의 실행시간이 벨만 포드(Bellman-Ford) 알고리즘의 실행 시간보다 빠릅니다.
다익스트라 알고리즘은 source s로부터 최종 최단 경로 가중치가 이미 결정된 노드의 집합 S를 갖습니다.
이 알고리즘은 반복적으로 최소값의 최단 경로 추정치를 가지는 노드 u (∈ V - S)를 선택하고 집합 S에 u를 더하며, u를 떠나는 모든 edges를 relax시키는 방식으로 동작합니다.
다음 구현에서 우리는 각 노드들의 d 값(distance)을 key로 하는 노드의 최소 우선순위 큐 Q를 사용합니다.
3-1. Dijkstra's algorithm 정리
- Bellman-Ford 와 마찬가지로 single-source shortest-paths를 구하는 알고리즘이다.
- 하지만 차이점은 모든 edge의 weight가 non-negative라는 것이다.
- 즉, w(u, v) >= 0
- 다익스트라 알고리즘은 벨만포드보다 running time 이 빠르다.
- 다익스트라 알고리즘은 집합 S를 유지한다.
- source부터의 shortest path가 이미 결정된 vertex의 집합
- 알고리즘을 돌리다 보면 이 set S에 한 노드씩 추가가 되고
- 알고리즘이 끝나면 모든 vertex가 set S에 들어가게 된다.
- 알고리즘을 돌리면서 아래와 같은 두 가지 동작을 반복한다.
-
- select: source부터의 distance가 현재까지 가장 작은 노드를 선택한다. -> 얘가 set S에 추가 됨
- relax (update): select을 통해 고른 vertex u에 대해 노드 u에서 출발하는 모든 vertex를 다시 relax 한다.
-
- 위 loop가 끝나면 모든 vertex에 대해서 relax가 끝나있게 된다.

- vertex가 5개 있는데 모든 vertex의 s로부터 distance는 무한대로 초기화한다.
- loop
- select:
- source로부터 distance가 가장 작은 노드는 s이기 때문에 s가 select 집합에 들어간다.
- s로부터 도달가능한 노드인 t, y에 대해 relax 진행
- t: s를 통해서 가는 경우 10에 갈 수 있으니 10으로 update
- y: s를 통해서 가는 경우 5에 갈 수 있으니 5로 update
- 이 과정이 끝나고 distance가 가장 작은 y가 set S에 들어간다. (s는 이미 select 됐으니 제외, y < t | 5 < 10)
- y에서 갈 수 있는 t, x,z에 대해 relax
- t: y를 통해 8에 가는 것으로 update
- x: y를 통해 14에 가는 것으로 update
- z: y를 통해 7에 가는 것으로 update
- 다시 s, y제외한 set S에 없는 애들 중에서 s로부터 distance값이 제일 작은 애를 set S에 넣는다. => z
- z를 통해 갈 수 있는 x 노드 relax:
- x -> 13으로 update
- set S에 t 대입, 그 다음 distance가 제일 작은 t를 통해 x 노드 relax
- x -> 9로 update
- 남은 것이 x밖에 없기 때문에 set S에 x 대입
- update 사항 없음
- select:
여기서 두 가지 의문점이 생길 수 있습니다.
- 이 경우 s로부터 distance가 가장 작은 애를 update 했는데 만약에 distance가 같은 애들끼리 있으면 어떻게 하나요?
- 뭘 먼저 해도 상관 없지만 -> 되도록 알파벳 순서대로 하는 것이 좋습니다.
- undirected(무방향)로 되어있는 경우는 어떻게 하나요?
- 모든 방향을 다 고려하여서 진행해야 합니다.
- undirect라고 다를 것은 없습니다. 기본적인 algorithm은 그대로 유지합니다.(select, relax)
3-2. pseudo code

- 1번줄에서 d와 π값을 보통 방식대로 초기화하고 2번 라인은 빈 집합 S를 초기화합니다.
- 4-8번 줄에서 while loop의 매 iteration 시작마다 Q = V - S 의 invariant를 유지합니다.
- 3번줄에서 최소 우선순위 큐 Q를 초기화합니다.
<진행과정>
- (bellman-ford와 유사하게) 모든 vertex를 initialize
- set S = 선언 및 초기화
- 현재 까지 distance가 제일 작은 애를 알아내기 위해서 min heap을 사용한다.(key = v.d)
- Q : min heap
- 즉, heap 구조에서 pop을 하면 s로부터 distance가 제일 작은 애가 나온다.
- while: Q에 남은 원소가 없을 때까지
- loop를 돌리면서 Q에서 노드를 하나씩 pop을 하고 이를 set S에 넣고
- pop한 노드 u에서 갈 수 있는 노드들에 대하여 relax 진행
그런데 위 pseudo code는 그대로 쓸 수 없는 이유가 하나 존재합니다.
그것은 바로 큐에 distance와 vertex name을 묶은 정보가 쭉 저장될텐데, while loop안의 for문에서 relax를 진행할 때, relax는 vertex 당 한 번만 진행합니다.
그런데 다익스트라 알고리즘은 집합 S에 더하는 작업을 위해서 {V - S}의 노드에서 항상 "lighest" 혹은 "closest" 노드를 선택하기 때문에, 우리는 이를 일종의 그리디 알고리즘이라고 할 수 있습니다.
그렇기에 각 EXTRACT-MIN 연산에서 O(logV)의 시간이 소요됩니다. 그러한 연산이 앞서 |V|번 존재합니다.
이진 최소 힙(binary min-heap)을 구축하는 데 드는 시간은 O(V)입니다.
각 DECREASE-KEY 연산은 O(logV) 시간을 소요하고 많아봐야 그러한 연산이 |E| 번만큼 존재합니다.
따라서 총 실행 시간은 O((V+E)logV)인데, 이는 모든 노드가 source로부터 도달가능하다는 전제하에 O(ElogV)입니다.
정리하면 다음과 같습니다.
- 다익스트라 알고리즘은 일종의 그리디 알고리즘에 해당된다.
- 현재까지 알려진 것 중에 가장 작은 노드를 기준으로 진행되어 최선의 선택을 하기 때문에 그렇다.
- 이 경우 항상 global optimum이 구해지는가? -> 그렇다. 하지만 증명이 굉장히 복잡하다.
- time complexity
- 5번 줄: O(VlogV)
- 7,8번: O(ElogV)
- 따라서 O(VlogV + ElogV) 인데 V >= E이기 때문에 최종적인 다익스트라 알고리즘의 time complexity는
- O(ElogV)
따라서 앞의 벨만포드는 O(EV)였기 때문에 벨만포드보다 더 빠른 시간복잡도를 가진다는 것이 증명되는 것입니다.
코드로 구현
from heapq import heappop, heappush
import math
def dijkstra(graph, source):
# initialize
distance = {}
predecessor = {}
for node in grpah.keys():
distance[node] = math.inf
predecessor[node] = None
distance[source] = 0
selected = set() # the set S
min_q = [(0, source)] # (distance from source, vertex name)
while min_q:
# u is selected and added to the set S
distance_u, u = heappop(min_q)
selected.add(u)
# w is the weight of edge (u, v)
# relax (u, v), if v is not selected
for v, w in graph[u].items():
if v not in selected: # selected가 안 된 애들의 경우에만 relax
if distance[v] > distance[u] + w:
distance[v] = distance[u] + w
predecessor[v] = u
heappush(min_q, (distance[v], v)) #update한 정보를 다시 q에 넣는다.
return distance, predecessor
Fig24_6 = {
's': {'t': 10, 'y': 5},
't': {'x': 1, 'y': 2},
'x': {'z': 4},
'y': {'t': 3, 'x': 9, 'z': 2},
'z': {'s': 7, 'x': 6}
}
dist, pre = dijkstra(Fig24_6, 's')
print(pre)
print(dist){'s': None, 't': 's', 'x': None, 'y': 's', 'z': None}
{'s': 0, 't': 10, 'x': inf, 'y': 5, 'z': inf}
node 이름이 string으로 되어있기 때문에 set으로 한 것입니다.
만약 node 이름이 integer라면 자동으로 리스트는 index가 붙기 때문에 그냥 리스트로 해서 메모리도 절약하고 속도도 증가시킬 수 있습니다.
- 리스트로 한다는 의미는 노드 수 만큼의 크기를 가지는 리스트를 생성해서 해당하는 노드의 number를 인덱스로 하는 리스트의 값을 0에서 1로 바꾸면 select 되었다라고 설정할 수 있습니다.
3-3. 다익스트라 알고리즘과 관련된 문제
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net

빨간줄의 의미는 딕셔너리보다 리스트로 하는 것이 더 유리하다는 것을 알려주는 정보이다.

def dijkstra(graph, source):
num = len(graph) - 1
distance = [math.inf] * (num+1)
distance[source] = 0
selected = [False] * (num+1)
min_q = [(0.0, source)]set S에 들어가면 selected가 True 가 된다.
0.0인 이유는 inf가 float이기 때문에 type을 맞춰주기 위함.
4. 정리 (다익스트라 vs. 벨만-포드)
다익스트라
1. 반복문을 통해 매번 방문하지 않은 노드들에 대해 최단 거리가 가장 짧은 노드를 min-heap priority로 찾아 relax를 진행해 나간다.
2. edge 중에 음수 가중치가 없어야 최적의 해를 찾을 수 있다.
3. O(ElogV)의 시간 복잡도
벨만-포드
1. |V-1| 번 반복문을 진행하며, 매 iteration 마다 모든 edge를 확인하면서 모든 노드 간 최단 거리를 구해 나간다.
2. 음수로 된 가중치가 있을 때 사용한다.
3. O(VE)의 시간복잡도
5. Topological sort (위상 정렬)
이번 섹션은 코딩테스트에 많이는 나오지 않지만 그래도 알아놓으면 좋은 위상 정렬입니다.
이는 우리가 어떻게 방향 비순환 그래프(Directed Acyclic Graph)의 topological sort(위상정렬)을 수행할 수 있을지를 보여줍니다. (Directed Acyclic Graph는 줄여서 DAG라고 부르기도 합니다.)
dag G = (V, E)의 위상 정렬은 만약 G가 edge(u, v)를 포함한다면 u는 순서상으로 v 이전에 보이도록 모든 노드들의 순서를 선형적으로 정렬하는 방법입니다. (만약 그래프가 cycle을 포함한다면 어떠한 linear ordering도 불가능하다.)
우리는 그래프의 위상정렬을 모든 방향 간선이 왼쪽에서 오른쪽으로 가도록 하는 지평선을 따르는 노드들의 순서로 볼 수 있습니다.
그래서 위상정렬은 우리가 생각하는 일반적인 "정렬(sorting)"의 종류와는 거리가 있습니다.
실제로 그래프를 사용하는 많은 곳에서는 사건을 따라 우선순위를 나타내는 DAG를 사용합니다.
아래 그림은 Professor Bumstead가 아침에 옷을 차려있을 때 발생하는 예제를 보여줍니다.
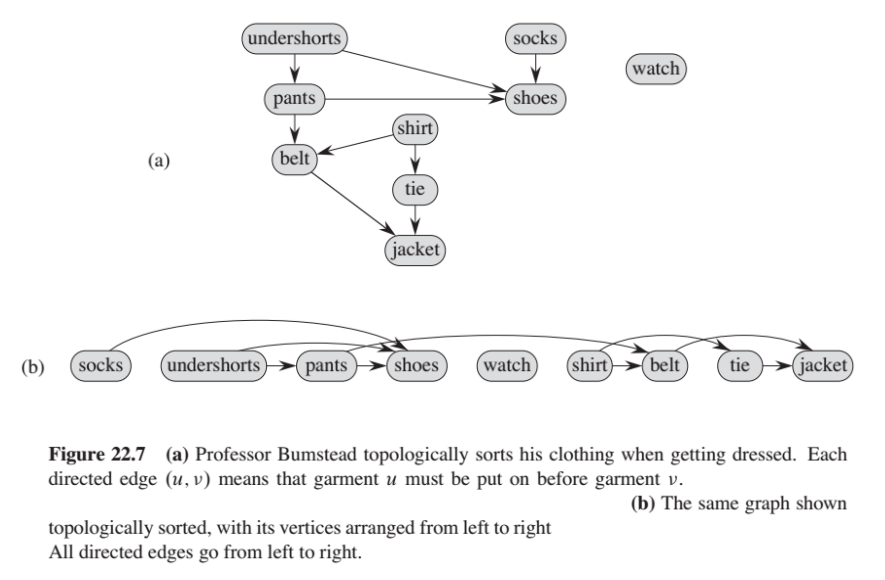
(a) Bumstead 교수는 옷을 차려입을 때 위상적으로 그의 옷을 정렬합니다. 각 방향 간선 (u, v)는 의복 u가 반드시 의복 v전에 입혀져야 한다는 것을 의미합니다. (즉, 양말: u | 신발: v)
(b) 마찬가지로 노드가 왼쪽에서 오른쪽으로 위상적으로 정렬된 그래프를 보여줍니다. 모든 방향 간선은 왼쪽에서 오른쪽 방향으로 진행됩니다.
from collectionㄴ import deque
import sys
items = ['undershorts', 'pants', 'belt', 'shirt', 'tie', 'jacket', 'socks',
'shoes', 'watch']
num = len(items)
# adjacency list
graph = [[1, 7], [2, 7], [5], [2, 4], [5], [], [7], [], []]
# compute indegree of each node
indegree = [0] * num
for i in range(num):
for j in range(len(graph[i])):
indegree[graph[i][j]] += 1
# enqueue the nodes of degree 0
q = deque()
for i in range(num):
if indegree[i] == 0:
q.append(i)
while len(q) > 0:
i = q.popleft() # process a node(item)
print(items[i])
for j in range(len(graph[i])): # process adjacent nodes
adj = graph[i][j]
indegree[adj] -= 1
if (indegree[adj] == 0):
q.append(adj)- indegree 변수는 본인에게 들어오는 edge의 갯수를 세는 역할을 합니다.
- 그래서 이후에 자신에게 들어오는 edge가 없다면 그 옷은 어떠한 것을 먼저 입어야 하는 제약이 없다는 것이기 때문에 바로 큐에 넣어줍니다.
- 반복문을 통해 큐에 들어간 값을 pop하여 프린트 합니다.(프린트 했다는 의미는 옷을 입었다는 의미)
- for문에서는 방금 입은 옷 다음에 입을 수 있는 옷들에 대해 하나씩 입어줍니다.
- 그러면 그 입을 수 있는 옷들의 indgree는 하나 줄어들 것이고 그랬을 때 그 옷에 대한 indegree 값이 없어지면, 즉 그 옷을 입기 전에 입어야 할 옷이 없다면 큐에 집어넣어주면 됩니다.
따라서 큐의 역할은 바로 집어서 입을 수 있는 옷들의 대기열이라고 생각하시면 됩니다.
7-1. 위상 정렬과 관련된 문제
2252번: 줄 세우기
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의
www.acmicpc.net


from collections import deque
import sys
sys.stdin = open('bj2252.txt', 'r')
N, M = map(int, input().split())
# build the adjacency list
graph = [[] for _ in range(N + 1)]
for _ in range(M):
a, b = map(int, sys.stdin.readling().split())
graph[a].append(b)
# compute indegree of each node
'CS 지식 > 자료구조와 알고리즘(Python)' 카테고리의 다른 글
| [자료구조와 알고리즘 | 파이썬] Greedy Algorithms(그리디 알고리즘) (1) | 2022.12.31 |
|---|---|
| [자료구조와 알고리즘 | 파이썬] Dynamic Programming(동적계획법) - 다이나믹 프로그래밍; DP (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Heaps (힙) 자료구조 (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Graphs - 그래프 자료구조(+약간의 python 개념) (1) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Trees (트리 자료구조) (0) | 2022.12.31 |
소중한 공감 감사합니다