[자료구조와 알고리즘 | 파이썬] Heaps (힙) 자료구조
2022.12.31- -
1. Heaps
heap을 이용하여 sorting을 하는 것을 heap sort라고 합니다.
heap이 주로 사용되는 곳은 priority queue(우선순위 큐)입니다.
2. Complete binary tree (완전 이진 트리)
완전 이진 트리는 그 높이에 대한 노드 수가 최대인 트리를 말합니다. 즉, 모든 레벨에서 노드들로 꽉 채워져 있는 것을 말합니다.
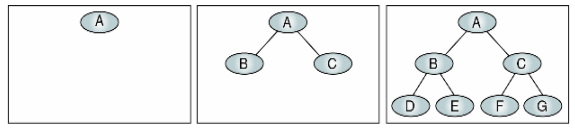
즉, 첫 번째 그림(height = 0) 에서 height 0에 대해 node를 maximum으로 채우는 경우는 오직 1개가 들어가는 구조입니다.
이진 트리(Binary tree)는 거의 완전합니다. 다음 두 조건만 만족한다면.
- 마지막 레벨을 제외하고 모든 노드가 채워진 트리 구조입니다.
- 노드는 왼쪽에서 오른쪽으로 채워져야 합니다.

Properties of Nearly complete binary trees: 특징

- h = ⌊log2N⌋
- 여기서 N은 노드의 개수이고 h는 트리의 높이 입니다.
- ⌊ x ⌋ means Gauss's notation: x를 넘지 않는 최대 정수
- Leaf node: ⌊N/2⌋ + 1, ⌊N/2⌋ + 2, ..., N
- 1 ~ ⌊N/2⌋: 자식노드를 가지는 internal node (leaf 노드가 아닌 노드)
- ⌊N/2⌋ + 1 ~ N: leaf node
- complete binary tree에서 N = 2h+1 – 1
Heaps
- Heap은 heap property를 만족하는 nearly complete binary tree이다.
- 두 종류의 이진 힙(binary heap)이 존재한다.
- max-heaps(최대힙)과 min-heaps(최소힙).
- 두 종류 모두 노드의 값이 heap property를 만족하며, heap property의 세부 사항은 heap의 종류에 따라 달라진다.
- max-heap에서 max-heap property는 루트를 제외한 모든 노드 i에 대해 다음과 같다:
- 어떤 root 노드의 값이 그 노드의 자식 노드의 값보다 항상 크거나 같다.
- A[Parent(i)] >= A[i],
- 즉, 한 노드의 value는 아무리 커도 기껏해야 부모 노드의 값이다. 따라서 max-heap에서 가장 큰 요소는 루트에 저장된다.
- 궁극적으로 max-heap에서 가장 큰 element는 root에 담겨있다.
- 어떤 root 노드의 값이 그 노드의 자식 노드의 값보다 항상 크거나 같다.
- min-heap은 그 반대로 구성되어 있다.
- 가장 작은 element가 min-heap의 root에 담겨 있다.


(a) 그림의 tree는 nearly complete binary tree이면서 max heap property를 만족합니다.
max-heap은 (a) 이진 트리와 (b) 배열로 보입니다. 트리의 각 노드에서 원 안의 숫자는 그 노드에 저장된 값입니다.
원 위의 숫자는 배열의 인덱스와 상응합니다.
(b) 그림에서 배열의 위 아래로 그어진 선들은 부모-자식 관계를 나타나는 것이며, 이는 배열에서 부모 인덱스는 는 항상 그들 자식의 왼쪽에 존재하게 됩니다.
Maintaining the heap property (heap property를 유지하기)
max-heap property를 유지하기 위해서 우리는 MAX_HEAPIFY 절차라고 부릅니다.
그것의 input은 배열 A와 배열에 대한 인덱스 i입니다. 호출될 때 MAX-HEAPIFY는 LEFT(i)과 RIGHT(i)에 루트 된 이진 트리가 max-heap이지만 A[i]가 자식 트리보다 작을 수 있기 때문에 max-heap property에 위배된다고 가정합니다.
MAX_HEAPIFY는 A[i]의 값이 max-heap에서 "float-down" 하도록 하여 인덱스 i에 루팅된 subtree가 max-heap property를 만족하도록 합니다.
- 어떤 node의 값을 max heap property를 만족하도록 구조를 조정하는 것


- max heap을 만들어야 하는데 2번 노드를 보니까 max heap property를 만족하지 않는 것을 볼 수 있다. (자식 노드보다 내가 더 크지 않음)
- heap property를 만족할 때까지 해당 노드를 끌어 내린다.
- 2번 노드와 그 자식 노드인 4번 노드의 값을 비교하여 자식 노드의 값이 더 크다면 두 노드의 값을 바꾼다.
- 또 다시 4번 노드를 확인하여 위의 과정을 진행한다.
- 만족하지 않기 때문에 4번 노드와 9번 노드의 값을 바꿔준다.
- 만족!
Building a heap (힙 만들기)
배열 A[1 ..n]을 변환하는 bottom-up(상향식) 방식으로 MAX_HEAPIFY 절차를 사용할 수 있습니다.
- max-heap의 경우 n = A.length


internal node 중에서 가장 큰 애부터 루트 노드까지에 대하여 Max- heapify를 진행한다.
Implementation of Max Heap
class MaxHeap:
def __init__(self, data_list = None):
self.h = [0] # the heap
if data_list is not None:
self.h.extend(data_list)
# build the max heap
# apply max_heapify() only for internal nodes
for i in range(self.size() // 2, 0, -1): # internal node의 제일 끝에 있는 애부터 root까지
self.max_heapify(i)a = [4, 8, 7, 2, 9, 10, 5, 1, 3, 6]
h1 = MaxHeap(a)
print(h1.h)
보면 리스트는 heapify가 되어 max-heap 형태가 된 것을 볼 수 있습니다.
# return the current size of the heap
def size(self):
return len(self.h) - 1 # 0 제외
# move item k as down as possible
def max_heapify(self, k): # k는 heapify를 진행할 노드 number
left = k * 2
right = k * 2 + 1
largest = k
if left <= self.size() and self.h[left] > self.h[largest]:
largest = left
if right <= self.size() and self.h[right] > self.h[largest]:
largest = right
if largest != k:
self.h[k], self.h[largest] = self.h[largest], self.h[k]
self.max_heapify(largest) # recursion- 재귀 함수를 통해 구현되기 때문에 현재 노드를 지칭하는 변수 k가 인자로 들어옵니다.
- 트리 구조에서 배웠듯이
- 왼쪽 노드의 인덱스 = k * 2
- 오른쪽 노드의 인덱스 = k * 2 + 1
- largest는 현재 부모 노드를 말하고 left node가 존재하면서(and) 그 left 노드가 부모 노드보다 크면 largest를 left로 바꾼다.(right도 마찬가지로)
- largest != k의 의미는 자식 노드 중에 자신보다 큰 값을 가진 노드가 있다는 의미이다. (만약 자신이 자식 노드들보다 큰 값을 가졌다면 largest 값이 바뀌지 않았을 것이기 때문) 그러므로 두 값을 바꿔준다.
- left를 먼저 확인하고 right를 확인하기 때문에 둘 다 max-heapify를 만족하지 않는 경우 마지막에 largest를 update한 right node와 교환을 진행한다.
- sub tree로 들어가기 위해서 재귀 호출을 진행한다

# max_heapify 한 번 진행할 때마다 바뀌는 과정
[4, 8, 7, 2, 9, 10, 5, 1, 3, 6] # 초기 배열
[0, 4, 8, 7, 2, 9, 10, 5, 1, 3, 6]
[0, 4, 8, 7, 3, 9, 10, 5, 1, 2, 6] 2-3
[0, 4, 8, 10, 3, 9, 7, 5, 1, 2, 6] 7-10
[0, 4, 9, 10, 3, 8, 7, 5, 1, 2, 6] 8-9
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6] 10-7-4(recursion)
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6]- 한 노드에 대해서 max-heapify를 돌리면 나오는 결과를 보여줌
- 10개의 노드가 있기 때문에 10//2(5) 부터 1까지 for문이 돈다. (5~1)
# 재귀 전까지 print()를 찍어본 것인데 참고
[0, 4, 8, 7, 2, 9, 10, 5, 1, 3, 6] # 초기 상태
[0, 4, 8, 7, 3, 9, 10, 5, 1, 2, 6] # 4번째 노드 (2,3 교환)
[0, 4, 8, 7, 3, 9, 10, 5, 1, 2, 6] # 재귀를 했지만 다음 노드가 없어서 변화 x
[0, 4, 8, 10, 3, 9, 7, 5, 1, 2, 6] # 3번째 노드 (7,10 교환)
[0, 4, 8, 10, 3, 9, 7, 5, 1, 2, 6] # 재귀를 했지만 다음 노드가 없어서 변화 x
[0, 4, 9, 10, 3, 8, 7, 5, 1, 2, 6] # 2번째 노드 (8,9 교환)
[0, 4, 9, 10, 3, 8, 7, 5, 1, 2, 6] # 재귀를 했지만 이미 만족하고 있어서 변화 x(9, 6)
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6] # 1번째 노드 (4, 10 교환)
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6] #
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6]
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6]- 아래 것이 맞는 거임(재귀까지 고려)
[0, 4, 8, 7, 2, 9, 10, 5, 1, 3, 6] # 초기 상태
[0, 4, 8, 7, 2, 9, 10, 5, 1, 3, 6]
[0, 4, 8, 7, 3, 9, 10, 5, 1, 2, 6] # 4번째 노드 (2,3 교환)
[0, 4, 8, 7, 3, 9, 10, 5, 1, 2, 6]
[0, 4, 8, 10, 3, 9, 7, 5, 1, 2, 6] # 3번째 노드 (7,10 교환)
[0, 4, 8, 10, 3, 9, 7, 5, 1, 2, 6]
[0, 4, 9, 10, 3, 8, 7, 5, 1, 2, 6] # 2번째 노드 (8,9 교환)
[0, 4, 9, 10, 3, 8, 7, 5, 1, 2, 6]
[0, 10, 9, 4, 3, 8, 7, 5, 1, 2, 6] # 1번째 노드 (4, 10 교환)
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6] # (재귀) 3번째 노드(4, 7 교환)
[0, 10, 9, 7, 3, 8, 4, 5, 1, 2, 6]
The heapsort algorithm (힙 정렬 알고리즘)
- asending order(오름차순)
내가 가진 값들 중 가장 큰 data를 가지는 노드는 항상 1번 index 일 것이다라는 아이디어를 이용합니다.


옅게 칠해진 회색 노드들 만이 heap 안에 남아 있는 것들입니다.
다음 과정과 같이 진행됩니다.
- 제일 큰 값인 1번 index(트리의 root)를 제일 작은 값인 마지막 index 간의 자리를 서로 바꾼다.(가장 큰 값 정렬 리스트에 추가)
- heap의 길이를 하나 줄인다.
- 이 과정을 통해 1번 index는 유일하게 heap property를 만족하지 않는 노드가 된다.
- 맨 위에 있는 1번 index의 노드(최솟값)를 MAX_HEAPIFY를 통해 아래로 끌어내린다.
- 그러고 다시 위의 3 과정을 계속해서 반복(재귀적으로)


root에서 계속 끌어 내리면서 하나씩 배열에 추가하다보면 그 배열은 자연스럽게 정렬된 배열이 됩니다.
이것이 바로 max-heap 구조와 heapify를 통한 정렬이라고 볼 수 있습니다.
앞서 만들어 둔 Heapify 클래스의 멤버 함수인 heap_sort를 구현해 보겠습니다.
def heap_sort(self):
save = self.h[:] # shallow copy
sorted_list = self.h[1:]
for i in range(self.size(), 0, -1): # 제일 마지막 노드부터
self.h[1], self.h[i] = self.h[i], self.h[1]
sorted_list[i - 1] = self.h[i] #제일 큰 걸 가져와서 list에 넣는다.
self.h.pop() #list에 넣은 건 제거
self.max_heapify(1) # root에 대한 heapify
self.h = save # 망가진 h 복구
return sorted_listprint(h1.heap_sort())
print(h1.h)
- heap 구조의 배열을 shallow copy를 통해 save해 두고, 정렬할 리스트로 사용할 리스트는 heap 배열의 0번 인덱스가 dummy index로 활용했었기 때문에 1번 인덱스부터 사용한다.
- 제일 마지막 노드부터 for문을 돈다.
- 현재 돌고 있는 노드가 트리의 루트 노드와 값을 바꿔준다.
- 정렬된 리스트의 현재 돌고 있는 노드의 인덱스에 맞는 위치에 heap에서의 값을 넣어준다.
- heap 배열에서 그 값을 pop한다.
- 루트 노드의 값이 바뀌어 max-heap 조건을 만족하지 않으므로 root 노드에 대한 heapify를 진행한다.
- save에 h를 copy를 하고나서 heapify를 진행하면 h에 대해 heapify가 진행되어 h가 망가졌을 것이기 때문에 저장했던 save를 h에 다시 복구해 준다.
- Q) save로 heap sort를 진행하고 41번 라인을 없애면 안되나?
- A) max-heapify는 클래스에 내장된 h를 이용하기 때문에 save에 대해서 heapify가 진행되지 않고 무조건 h로 heapify가 진행된다. 그래서 root 노드와 가장 마지막 노드를 바꾸는 것 까지는 되지만 제일 중요한 heapify를 못하기 때문이다.
Priority queues (우선순위 큐)
이 섹션에서는 heap의 가장 일반적인 적용 사례 중 하나를 소개합니다:
- efficient priority queue.
heap과 마찬가지로 우선순위 큐는 두 가지 형태로 제공됩니다.
- max-priority queues(최대 우선순위 큐)
- min-priority queues.(최소 우선순위 큐)
우선순위 큐는 각각 key라고 불리는 연관된 값을 가진 요소들의 집합 S를 유지하기 위한 자료구조입니다. max-priority queue는 다음 연산을 지원합니다.
- INSERT(S, x)
- 원소 x를 집합 S로 삽입한다. 표현식은 아래와 같다.

- MAXIMUM(S)
- 가장 큰 key값을 가진 S의 원소를 반환한다.
- EXTRACT-MAX(S)
- 가장 큰 key를 가진 S의 원소를 반환하며, 제거한다. (추출)
HEAP-EXTRACT-MAX
<psuedo code>
#HEAP-EXTRACT-MAX(A) # max heap 리스트
if A.heap_size < 1: # 1
error "heap underflow"
max = A[1]
A[1] = A[A.heap_size] # 제일 끝에 있는 노드를 제일 첫 노드에 넣는다.
A.heap_size = A.heap_size - 1 # heap size를 하나 줄인다.
MAX-HEAPIFY(A, 1) # 제일 위에 있는 노드는 heap property를 만족하지 않으므로 끌어 내린다.
return max # 7
위는 heap sort에서 배운 메커니즘과 동일합니다.
def pop(self):
if self.size() == 0:
return None
item = self.h[1]
# copy the last item to root and remove it
self.h[1] = self.h[self.size()]
self.h.pop()
self.max_heapify(1)
return itemfor _ in range(h1.size()):
print(h1.pop(), end=' ')
print()
print(h1.h)
- 힙의 크기가 0이면 None을 반환
- 1번 인덱스로부터 item을 가져옴(제일 큰 값)
- 가장 마지막 인덱스에 있는 값을 1번 인덱스로 끌어옴
- heap 배열에서 pop을 진행함
- 1번 인덱스에 대해 heapify
- item 반환
procedure MAX-HEAP-INSERT
데이터를 추가할 때는 그냥 집어 넣으면 안 되고 적절히 자기 자리를 찾아서 넣어주어야 합니다.

- heap property를 만족하도록 15를 추가하려고 한다.
- 새로 추가할 노드를 무조건 맨 밑, 맨 왼쪽에 붙인다. -> 항상 nearly complete binary tree (heap) 만족
- 붙인 15를 heap property를 만족하도록 위로 올린다. (heapify)
- 위로 올리는 과정은 아래로 내리는 heapify보다 더 쉽다.
- 아래로 내리면 두 자식 노드와 비교해야 하는데,
- 위로 올리는 과정은 부모 노드랑만 비교하면 되기 때문에 (부모 노드보다 크면 자식 노드보다는 무조건 클 것이기 때문에)
def insert(self, item):
self.h.append(item)
# move up the item to keep the max-heap property
k = self.size()
while k > 1 and self.h[k] > self.h[k//2]:
self.h[k], self.h[k//2] = self.h[k//2], self.h[k]
k //= 2 # 내 index를 부모 node index와 바꿈.h1 = MaxHeap()
for d in (4, 8, 7, 2, 9, 10, 5, 1, 3, 6):
h1.insert(d)
print(h1.h)
- 먼저 heap의 제일 마지막에 붙이면 되기 때문에 그냥 append를 하고
- heap이 비지 않았으면서(and) 새로 추가하는 노드(k)가 부모 노드(k//2)보다 크다면 둘이 바꿔줘야 한다.
- 바꿔주고 나서 내 인덱스를 바꾼 기존의 부모 위치로 update해서 반복문을 계속 돌면서 올라간다.
- 이 과정을 거치면 새로 추가하는 노드는 자기의 위치를 찾아갈 것이다.
Time Complexity of Building a Heap (Heap을 구축하는 데 드는 시간복잡도)
MaxHeap()의 time complexity는 어떻게 될까요?
MAX_HEAPIFY에 대한 각 호출은 O(logn) 시간이 소요되며, BUILD-MAX-HEAP는 O(n)에 해당하는 시간이 소요됩니다.
- 따라서 실행시간은 O(nlogn).
- BUILD-MAX-HEAP -> internal node의 가장 큰 애부터 root node까지 max-heapify를 진행하는 과정
- MAX-HEAPIFY -> root 노드부터 시작해서 재귀적으로 heapify
- BUILD-MAX-HEAP -> internal node의 가장 큰 애부터 root node까지 max-heapify를 진행하는 과정
이 상한은 정확하지만 점근적으로 딱 들어맞지는 않습니다.
MAX-HEAPIFY가 노드에서 실행된 시간은 트리의 height에 따라 달라지며 대부분의 노드 height 값이 작다는 것을 관찰함으로써 더 엄격한 경계(bound)를 설정할 수 있습니다.
우리의 철저한 분석은 n개 원소를 가진 heap에 대해 높이 ⌊logn] 그리고 어떤 높이 h에서 최대 [n/2h+1⌉ 개의 노드를 갖는 특성에 의존합니다.
⌊log2N⌋ ⌈ − ⌉
- ⌈n/2h+1⌉-> 반올림(ceiling)
- 각 층(height)에 있을 수 있는 노드의 최대 갯수를 의미한다.
- height = ⌊logn⌋ -> 가우스 (괄호에서 위가 잘림 - ㄴ 모양)
- 이는 n개 요소에 대한 트리의 height를 의미한다.
- 제일 아래 층 → n = 1 → log1 → h = 0
최악의 시간 복잡도

- 앞에 곱해지는 term
- Max heapify에서 loop를 도는 최대 횟수
- 0층은 leaf node이므로 loop를 0번 도는 것이고
- 1층은 그 위층의 노드로 0층에 대한 loop를 1번 돌면 된다.
- 뒤에 곱해지는 term(ex.⌈n/2⌉ by 위에 있는 n/2h+1)
- n/2 : h=0에 있을 수 있는 노드의 최대 갯수
- n/4: h=1에 있을 수 있는 노드의 최대 갯수
높이 h의 노드에서 호출될 때, MAX_HEAPIFY가 요구하는 시간은 O(h)이므로, 우리는 위에서 제한된 BUILD-MAX-HEAP의 총 cost를 O(h)로 표현할 수 있습니다.
→ O(h) : max-heapify에서 loop를 도는 횟수
- 0, 1, 2, .... 를 묶어 놓은 것

- 오른쪽 항의 n뒤에 붙은 sum의 의미는 n이 어떤 값을 갖던지 상관없이 2보다 작거나 같은 상수를 뜻한다.
- O(n) 으로 퉁칠 수 있음

위 식에서 x = 1/2로 대체하여 마지막 합계를 평가합니다.


따라서 우리는 BUILD-MAX-HEAP의 실행 시간을 다음과 같이 제한할 수 있습니다.

Why should one ever use a heap instead of a sorted array?
정렬된 배열 대신 힙을 사용해야 하는 이유?
맞습니다. 힙을 작성하는 데는 선형적인 시간이 걸리고 삽입/삭제 연산에는 O(logn)이 걸립니다. 최소/최대 저장 요소를 찾는 즉, heap을 peek하는 것은 물론 O(1)이며, head를 pop하는 것은 O(logn)입니다.
질문에 대한 답은 간단합니다. 일부 사용 사례에서는 모든 데이터를 정렬하는 것은 중요하지 않지만, 가장 작은/큰 요소를 지속적으로 유지하는 것은 중요합니다. 이는 많은 적용 사례에서 광범위하게 사용되는 개념인 우선순위 큐(Priority Queue)에 해당하는 것입니다.
- 삽입을 하는 상황에서
- sorted list의 경우 -> O(n)
- 하나하나 밀어야 되니까
- priority queue의 경우 -> O(logn)
- sorted list의 경우 -> O(n)
- 큰 데이터를 뽑아내야 하는 상황에서
- sorting의 경우, 정렬을 하는데 O(nlogn)이고
- priority queue의 경우 O(n)이기 때문에 prioriy queue가 훨씬 빠르다.
heapq - HEAP queue algorithm : 파이썬 내장 모듈 heapq
python 내장 heap module
1. heapq.heappush(heap, item)
- heap invariant를 유지하면서 value itme을 heap에 push 합니다.
- 즉, insert 하는 함수
- 값이 제일 작은 애가 제일 앞에 나와있는 구조
2. heapq.heappop(heap)
- heap에서 가장 작은 item을 pop하고 반환하여 heap invariant를 유지합니다. heap이 비어있으면 "IndexError"가 발생합니다.
- 제일 앞에 있는 놈을 추출
- 가장 작은 item을 pop하지 않고 access 하려면 heap[0] 을 사용합니다.
3. heapq.heappushpop(heap, item)
- heap에서 item을 push한 다음, heap에서 가장 작은 item을 pop하여 반환합니다.
- 이 결합된 작업은 heappush()이후에 heappop()에 대한 별도의 호출이 뒤따르는 것보다 더 효율적으로 실행됩니다.
- item을 insert하고, 제일 앞에 있는 data를 pop
4. heapq.heapify(x)
- 리스트 x를 linear time 내에 heap으로 변환합니다.
- 주의할 점: 파이썬 모듈 heapq는 minheap 이라는 점이다. (우리가 배운 maxheap과 다르게)
아래 링크를 통해 heapq 모듈에 대한 자세한 사용법을 보실 수 있습니다.
heapq — Heap queue algorithm — Python 3.8.14 documentation
heapq — Heap queue algorithm Source code: Lib/heapq.py This module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm. Heaps are binary trees for which every parent node has a value less than or equal to an
docs.python.org
import heapq
# A heap sort algorithm
def heapsort(iterable):
h = []
for value in iterable: # heapify 하는 과정
heapq.heappush(h, value)
return [heapq.heappop(h) for _ in range(len(h))] # sorting 과정
# You can transform a populated list into a heap
a = [3, 5, 1, 2, 6, 8, 7]
heapq.heapify(a)
print(a)
print(heapsort(a))
# Or use a list initialized to []
# Heap elements can be tuples.
b = []
heapq.heappush(b, (5, 'write code'))
heapq.heappush(b, (7, 'release product'))
heapq.heappush(b, (1, 'write spec'))
print(heapq.heappop(b))
실행 결과
[1, 2, 3, 5, 6, 8, 7]
[1, 2, 3, 5, 6, 7, 8]
(1, 'write spec')- 튜플로 heap data가 구성되는 경우 무조건 맨 앞에 있는 element를 기준으로 우선순위가 결정 된다.
- 그래서 가장 작은 값을 가지는 1의 튜플을 반환한다.(min-heap이기 때문에)
- (별첨)max-heapify 되는 과정
[0, 3, 5, 1, 2, 6, 8, 7]
[0, 3, 5, 8, 2, 6, 1, 7]
[0, 3, 5, 8, 2, 6, 1, 7]
[0, 3, 6, 8, 2, 5, 1, 7]
[0, 3, 6, 8, 2, 5, 1, 7]
[0, 8, 6, 3, 2, 5, 1, 7]
[0, 8, 6, 7, 2, 5, 1, 3]
- heap의 크기가 7이므로 7//2 = 3번부터 1번까지 max-heapify가 진행된다.
관련된 문제
14235번: 크리스마스 선물
크리스마스에는 산타가 착한 아이들에게 선물을 나눠준다. 올해도 산타는 선물을 나눠주기 위해 많은 노력을 하고 있는데, 전세계를 돌아댕기며 착한 아이들에게 선물을 나눠줄 것이다. 하지만
www.acmicpc.net


- max heap으로 priority queue를 만들어서 큐가 비었으면 -1 아니면 queue에서 꺼내서 준다.
- python은 minheap이기 때문에 max heap으로 하기 위해서는 queue에 저장할 데이터를 저장할 때 -를 붙였다가 다시 출력할 때 -를 붙여주면 된다.
- 2개를 충전하는데 첫번째는 3짜리 두번째는 2짜리
- 우선순위로 3을 먼저 줄 것이다.
import heapq
import sys
sys.stdin = open('bj14235_in.txt', 'r')
n = int(input())
present = []
for i in range(n):
a = list(map(int, input().split()))
if a[0] == 0:
if len(present) == 0:
print(-1)
else:
tmp = -heapq.heappop(present)
print(tmp)
else:
for j in range(a[0]):
heapq.heappush(present, -a[j+1])
14241번: 슬라임 합치기
영선이와 효빈이는 슬라임을 합치는 게임을 하고 있다. 두 사람은 두 슬라임을 골라서 하나로 합쳐야 한다. 게임은 슬라임이 하나 남았을 때 끝난다. 모든 슬라임은 양수 크기를 가지고 있다. 두
www.acmicpc.net


- 큰 점수를 얻으려면 최대한 먼저 큰 놈끼리 합쳐야 한다.
- queue에 데이터가 하나 남을 때까지 반복
- 두 놈을 꺼내서 점수 계산하고 합친 놈을 다시 queue에 넣고
'CS 지식 > 자료구조와 알고리즘(Python)' 카테고리의 다른 글
| [자료구조와 알고리즘 | 파이썬] Greedy Algorithms(그리디 알고리즘) (1) | 2022.12.31 |
|---|---|
| [자료구조와 알고리즘 | 파이썬] Dynamic Programming(동적계획법) - 다이나믹 프로그래밍; DP (2) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Graphs - 그래프 자료구조(+약간의 python 개념) (1) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Trees (트리 자료구조) (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Stacks and Queues (스택 & 큐) (0) | 2022.12.31 |
소중한 공감 감사합니다