[자료구조와 알고리즘 | 파이썬] Stacks and Queues (스택 & 큐)
2022.12.31- -
1. Stack ADT(스택)
1-1. Stacks(스택)
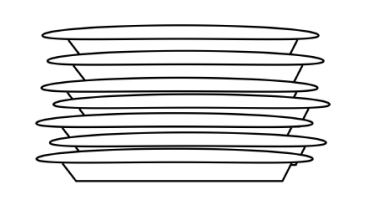
stack은 부엌에서 접시를 쌓는 것과 유사한 방식으로 data를 저장하는 자료구조입니다.
우리는 스택의 제일 윗 부분(top)에 접시를 둘 수 있고, 접시가 필요할 때 이 스택의 제일 윗 부분(top)으로부터 가져올 수 있습니다. 즉, 스택에 추가되는 마지막 접시는 그 스택으로부터 제일 먼저 집어 들어지는 것입니다.
이와 유사하게 stack 자료구조는 우리로 하여금 하나의 말단(end)으로부터 data를 읽고 저장할 수 있게끔 해주고 마지막에 추가되는 element가 첫 번째로 집어집니다.
따라서, stack은 last in, first out(즉, LIFO) 구조라고 합니다.
1-2. Basic operations(기본 연산)
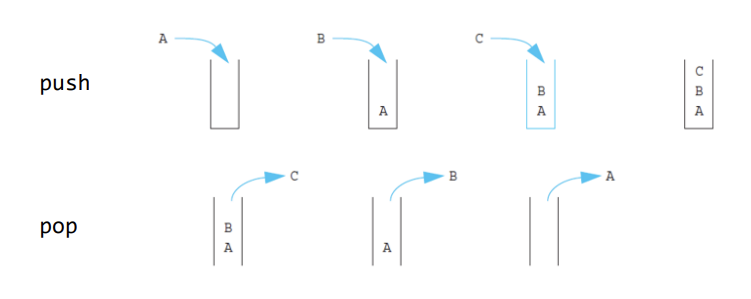
stack구조에서 INSERT(삽입) operation은 Push라고 불리고 DELETE operation은 element 인자를 받지않는 것으로 POP이라고 불립니다.
1-3. Stack implementation using Linked list(연결 리스트를 사용한 스택 구현)

class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class Stack:
def __init__(self):
self.top = None
self.size = 0Stack을 사용하기 위해서는 Stack object(instance)를 만들고 해당 object를 통해 stack class의 변수 및 함수에 접근합니다.
연결리스트는 노드를 기반으로 하기 때문에 노드 또한 구현되어 있습니다.
1-4. Push operation
아래 코드에서 self가 의미하는 것은 현재 method가 갖고 있는 object 자체를 의미한다.
def push(self, data):
node = Node(data)
if self.top: #스택이 비어있지 않다면
node.next = self.top # 1
self.top = node # 2
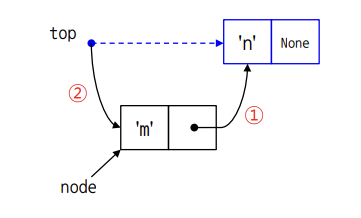
sefl.size += 1- 가장 먼저, 저장할 data를 갖고 있는 Node 객체를 하나 만든다.
- 이제 이 node를 stack 구조에 넣어야 할 차례이다.
- if self.top:이 의미하는 것은 스택이 현재 비어 있지 않는지를 물어보는 것이다.(비어있다면 top은 null일 것이기 때문에)
- 스택이 만약 비어있지 않다면 top을 새로 생성한 node의 next pointer가 가리키도록 한다.
- 스택이 만약 비어있다면 top이 새로 만든 node를 가리키게 한다.
1-5. Pop operation
def pop(self):
if self.size == 0:
return None
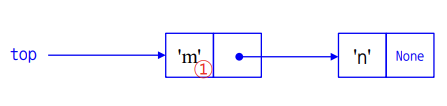
data = self.top.data # 1
self.top = self.top.next # 2
self.size -= 1
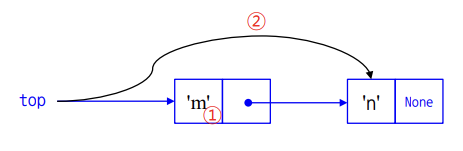
return data1. top에 위치하던 노드의 data 값을 변수에 일단 저장하고
2. top이 원래 가리키던 노드의 다음 노드를 가리킨다.
3. size 1 감소
4. 앞서 저장한 데이터 반환
1-6. Peek operation
def peek(self):
if self.size == 0:
return None
return self.top.data스택의 구조를 바꾸지 않고 top의 값을 반환하기만 하면 됩니다.
전체 코드
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class Stack:
def __init__(self):
self.top = None
self.size = 0
def push(self, data):
node = Node(data)
if self.top: #스택이 비어있지 않다면
node.next = self.top # 1
self.top = node # 2
sefl.size += 1
def pop(self):
if self.size == 0:
return None
data = self.top.data # 1
self.top = self.top.next # 2
self.size -= 1
return data
def peek(self):
if self.size == 0:
return None
return self.top.data
1-7. Bracket-matching application(괄호 매칭 프로그램)
이제 stack 구현을 어떻게 할 수 있는지를 보여주기 위한 예제를 살펴보겠습니다.
괄호 검사
def check_brackets(statement):
stack = Stack()
for ch in statement:
if ch in ('{', "[", '('):
stack.push(ch)
if ch in ('}', ']', ')'):
last = stack.pop()
if last == '{' and ch == '}':
continue
elif last == '[' and ch == ']':
continue
elif last == '(' and ch == ')':
continue
else:
return False
if stack.size > 0:
return False
else:
return True
sl = ("{(foo)(bar)}[hello](((this)is)a)test",
"{(foo)(bar)}[hello](((this)is)a test)",
"{(foo)(bar)}[hello](((this)is)a)test((")
for s in sl:
m = check_brackets(s)
print("{}: {}".format(s, m)){(foo)(bar)}[hello](((this)is)a)test: True
{(foo)(bar)}[hello](((this)is)a test): True
{(foo)(bar)}[hello](((this)is)a)test((: False- 열린 괄호의 경우 스택에 push하고 닫힌 괄호의 경우 pop 합니다.
- 여기서 pop 해서 나온 괄호가 가장 최근에 열린 괄호인데 두 괄호의 종류가 다른 경우 False를 반환합니다.
- 모든 문자열에 대해 for문을 진행하고 나서 스택에 남아 있는 괄호가 있는 경우 False를 반환합니다.
- 아무것도 해당하지 않았다면 True를 반환합니다.
1-8. Stack implementation using Python list(파이썬 리스트를 사용한 스택 구현)
data = "nse*a*qys** **eu***ot*i***"
stack = []
for ch in data:
if ch == '*':
print(stack.pop(), end='')
else:
stack.append(ch)python의 list와 관련된 method를 적절히 사용하여서도 stack구조를 충분히 구현해 낼 수 있습니다.
1-9. 관련된 문제
9012번: 괄호
괄호 문자열(Parenthesis String, PS)은 두 개의 괄호 기호인 ‘(’ 와 ‘)’ 만으로 구성되어 있는 문자열이다. 그 중에서 괄호의 모양이 바르게 구성된 문자열을 올바른 괄호 문자열(Valid PS, VPS)이라고
www.acmicpc.net
풀이
# 리스트 사용
def solution():
stack = []
string = input()
for i in string:
if len(stack) == 0 and i == ')':
print("NO")
return
if i == '(':
stack.append(i)
elif i == ')' and len(stack) != 0:
stack.pop()
if len(stack) == 0:
print("YES")
return
else:
print("NO")
return
test_case = int(input())
for _ in range(test_case):
solution()# 스택 사용
tc = int(input())
for _ in range(tc):
s = Stack()
test = input()
for ch in test:
if ch == '(':
s.push(ch)
elif ch == ')' and s.size != 0:
s.pop()
if s.size == 0:
print("YES")
else:
print("NO")
- 스택을 계속해서 만들기 때문에 메모리 낭비일 것 같다고 스택을 새로 만들지 않고 쓰던 걸 계속 사용하면 스택 안에 값이 남아있게 되는 문제가 발생할 수 있습니다.
- 즉, 한 test case를 진행 할 때마다 Stack()를 만들어주는 이유는 한 스택을 계속해서 사용하게 되면 스택이 비어있지 않은 경우가 발생할 수 있기 때문입니다.
Stack Implementation in C (C 언어로 구현한 스택)
스택 구조 자체에 더 잘 이해하기 위해서 C언어를 통해 구현해 보겠습니다.
Array implementation (배열 구현)
아래 그림에서 볼 수 있듯이, S[1...n] 라는 배열에서 최대 n개의 원소를 가진 stack을 구현할 수 있습니다.
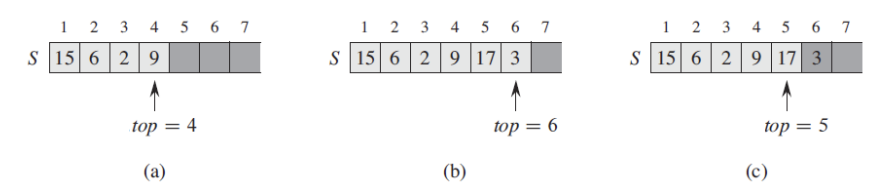
- S 스택의 배열 구현.
- 스택 원소는 옅게 칠해진 회색 위치에만 보인다.
- index는 1부터 시작(계산하기 편하도록)
(a)
- Stack S는 4개의 원소를 가진다.
- top 원소의 값은 9
(b)
- Push(S, 17)와 Push(S, 3) 를 호출한 후의 Stack S 모습이다.
(c)
- Pop(S)을 호출한 후 Stack S는 가장 최근에 pushed 된 요소 3을 반환하였다.
- 비록 배열에 3이라는 요소가 여전히 보이겠지만, 얘는 더 이상 stack 안에 있는 것이 아닌 취급을 한다.
- top element는 17
위 과정을 통해 알 수 있듯이, pop이라는 method는 배열 안의 값을 실제로 삭제할 필요없이 top의 위치만으로 삭제라는 기능을 간접적으로 구현할 수 있는 것입니다. (top 이후의 index에 값이 실제로 있더라도 없는 것처럼 생각하는 것이다.)
top = 0 일 때, stack은 어떠한 원소도 포함하지 않고 비어있는 것입니다.
query operation 인 STACK-EMPTY에 의해 stack이 비어 있는지 테스트해 볼 수 있습니다. 만약, 빈 stack을 pop하려고 시도하면 'stack이 underflow 되었다'고 하며, 이는 보통 error로 다루어 집니다.
또한, 만약 top이 n을 초과하였다면 'stack이 overflow 되었다' 하고 이 역시도 error로 다루어 집니다.
C코드 구현
#include <stdio.h>
#include <stdlib.h>
#define N 100
char stack[N + 1];
int top = 0;
int is_empty();
{
return top == 0;
}
int is_full();
{
return top = N;
}
void push(char item){
if (is_full()) {
printf("stack overflow\n");
exit(1);
}
stack[++top] = item;
}
char pop() {
if (is_empty()) {
printf("stack underflow\n");
exit(1);
}
return stack[top--];
}
int main()
{
char *data = "nse*a*qys** **eu***ot*i***";
for (; *data; data++) {
if (*data == '*')
printf("%c", pop());
else
push(*data);
}
printf("\n");
return 0;
}nsea qyseyutoi
Linked-list implementation (연결리스트 구현)

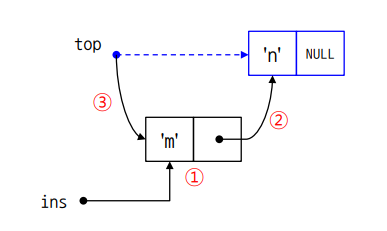
push
pop
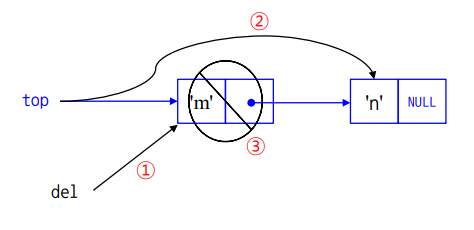
삭제할 노드를 del이라는 변수로 지칭하여 해당 노드 next 노드를 top이 가리킵니다.
#include <stdio.h>
#include <stdlib.h>
typedef struct _Node {
char data;
struct _Node *next;
} Node;
Node *top = NULL; //stack top
int is_empty()
{
return top == NULL;
}
void push(char item)
{
Node *ins;
ins = (Node *) malloc(sizeof(Node));
ins -> data = item;
ins -> next = NULL;
if(!is_empty())
ins -> next = top;
top = ins;
}
char pop()
{
Node *del;
char item;
if (is_empty()) {
printf("stack underflow!\n");
exit(1);
}
item = top->data;
del = top;
top = del->next;
free(del);
return item;
}
2. Queue ADT
2-1. Queues(큐)
queue는 다음과 같이 동작합니다.
- queue에 참석한 첫 번째 사람은 대개 첫 번째로 음식을 받는다.
- 그리고 모든사람은 그들 각자가 queue에 어떻게 참가했는지의 순서에 따라 음식을 받을 것이다.
- FIFO가 queue의 개념을 가장 잘 설명한다.
- FIFO: first in, first out(선입 선출)
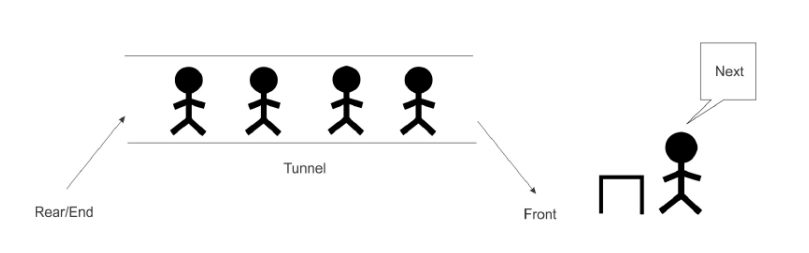
2-2. Basic operation(기본 연산)
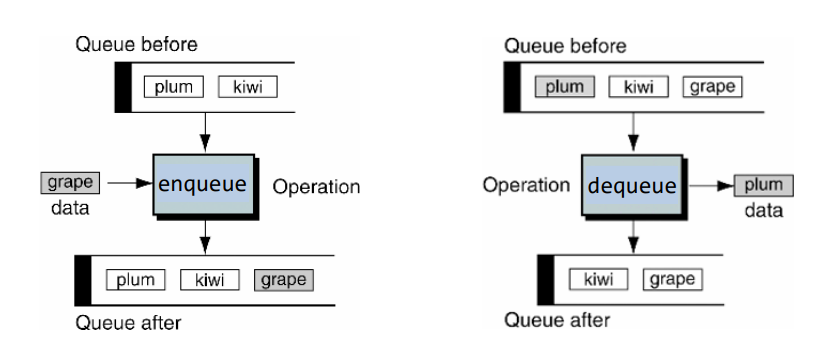
2-3. Queue implementation using Linked list(연결리스트를 사용한 큐 구현)
Linked list로 구현하는 Queue는 tail 포인터를 이용하여 데이터를 집어넣고(enqueue 연산),
head를 통해 데이터를 제거한다.(dequeue 연산)
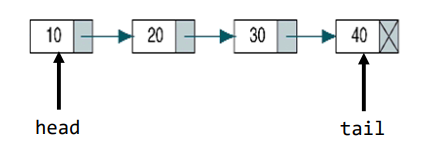
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class Queue:
def __init__(self):
self.head = None
self.tail = None
self.size = 0
2-4. The enqueue operation
def enqueue(self, data):
node = Node(data)
if self.size == 0: # 큐가 비어있는 경우
self.head = node
self.tail = node
else:
self.tail.next = node
self.tail = node
self.size += 1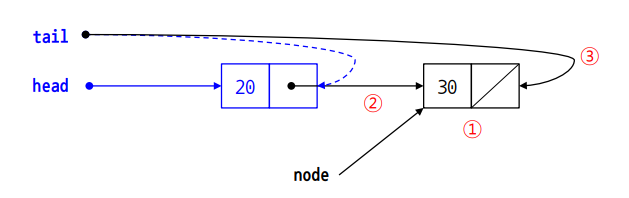
- node 변수에 data를 가진 노드 instance 하나를 생성해 집어 넣는다.
- 큐가 비어있는 경우
- head 노드와 tail노드 모두 생성한 노드를 가리킨다.
- 그렇지 않은 경우
- tail 노드의 next pointer가 새 노드를 가리키게 한다.
- 새 노드를 tail 노드로 바꾼다.
- size 1 증가
2-5. The dequeue operation
def dequeue(self):
if self.size == 0:
return None
self.size -= 1
data = self.head.data
self.head = self.head.next
return data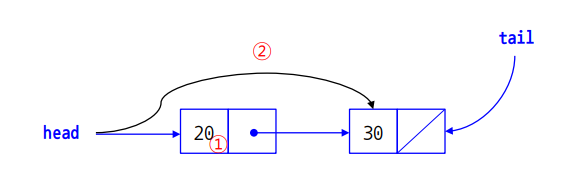
- 큐가 빈 경우에는 당연히 None 객체 리턴
- 그렇지 않은 경우
- size 1 감소
- data 변수에 head 노드의 data 대입
- head 노드의 next 포인터가 가리키던 노드를 head 노드로 변경
- data 반환
2-6. Python Deque (파이선 deque 모듈 -> 중요!)
파이썬에는 스택과 큐 자료구조를 모두 쉽게 다룰 수 있는 collections 모듈의 deque 클래스가 존재합니다.
사용 방법은 굉장히 간단합니다.
새로운 deque을 만들 때는 deque() 를 하면 되고 기존의 리스트를 deque으로 바꾸고 싶으면 괄호 안에 해당 리스트를 인자로 넣어주면 됩니다.
deque에서 사용되는 메소드는 아래 표로 정리해 두었습니다.
from collections import deque
deq = deque([1, 2, 3])
deq.append(4)
deq.appendleft(5)
print(deq)
print(deq.pop())
print(deq.popleft())deque([5, 1, 2, 3, 4])
4
5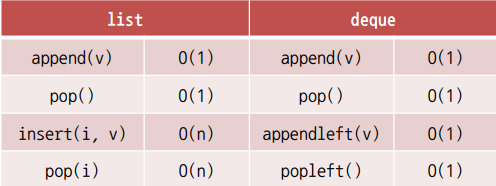
list의 경우 삽입과 삭제의 경우 리스트의 값들을 한 칸씩 밀어야 되기 때문에 O(n)의 시간 복잡도를 갖고
deque의 경우 linked list로 구현이 되어 있기 때문에 노드들 간의 연결만 바꾸어 주면 되므로 O(1)의 시간 복잡도를 갖습니다.
2-7. Queue implementation using Python deque (파이썬 deque를 사용한 큐 구현)
from collections import deque
data = "ea*sy **q*ue***st*i*on****"
queue = deque()
for ch in data:
if ch == '*' and len(queue) > 0:
print(queue.popleft(), end='')
else:
queue.append(ch)easy question파이썬에서 큐를 사용해야 하는 경우 앞서 구현한 것처럼 노드를 직접 만들어 사용할 수 도 있지만 이미 만들어져 있는 모듈을 사용하면 시간 단축에 탁월한 선택이 됩니다.
해당 모듈은 기본 내장 모듈로 코딩테스트 시에 사용해도 무방하기 때문에 굉장히 자주 사용되는 모듈이라고 할 수 있겠습니다.
스택과 큐 자체적인 문제는 크게 어렵지 않지만 나중에 나올 그래프 순회 방식의 DFS, BFS에서 각각 스택과 큐로 구현하기 때문에 이에 대해서 잘 알아두면 쓸모있게 사용할 수 있을 것으로 예상됩니다.
관련된 문제
2164번: 카드2
N장의 카드가 있다. 각각의 카드는 차례로 1부터 N까지의 번호가 붙어 있으며, 1번 카드가 제일 위에, N번 카드가 제일 아래인 상태로 순서대로 카드가 놓여 있다. 이제 다음과 같은 동작을 카드가
www.acmicpc.net
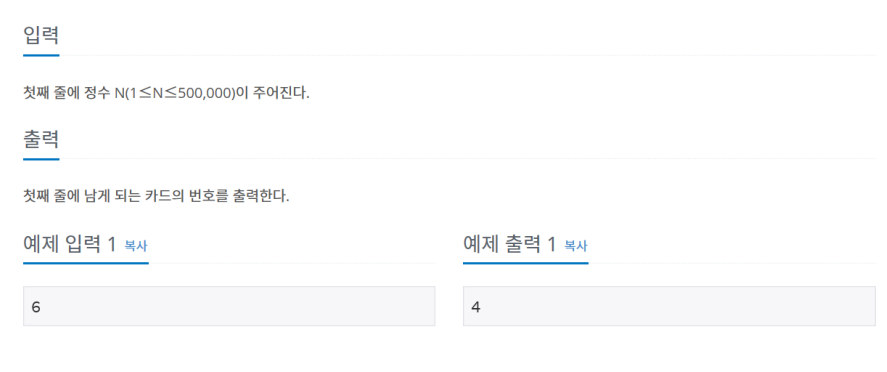
정답 코드
from collections import deque
n = int(input())
a = [i for i in range(1, n + 1)]
q = deque(a)
while len(q) != 1:
q.popleft()
num = q.popleft()
q.append(num)
print(a[0])
Queue implementation in C (C언어로 구현한 큐)
Array implementation(배열 구현)
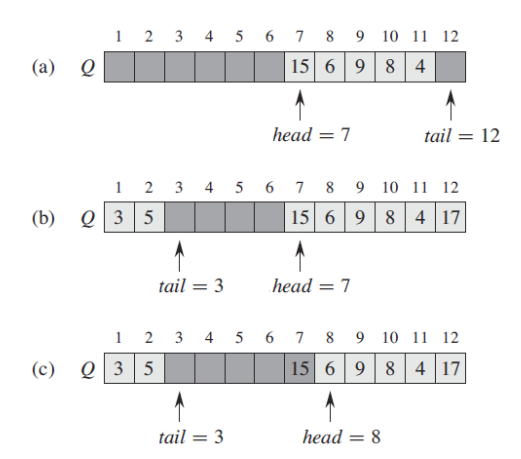
queue안의 원소들은 head, head+1, ..... tail - 1 과 같이 특정 주소에 위치하고 있고 그러한 구조 안에서 우리는 location 1이 location n을 바로 뒤따라 가고 있는 circular order(원형 순서) 라는 점을 이해하면 되겠습니다.
head=tail 일 때, 'queue는 비어있다'라고 생각합니다.
처음에 우리는 head = tail = 1로 설정합니다.
만약 빈 queue로부터 원소를 dequeue하려고 한다면, queue underflows가 발생할 것이고,
head = tail + 1일 때, queue는 가득 차 있는데 만약 element를 enqueue하려고 한다면 queue는 overflows가 발생합니다.
우리는 array1의 size를 클라이언트가 queue에서 보고자 하는 원소의 최대값보다 더 크도록 만듭니다.
#include <stdio.h>
#include <stdlib.h>
#define N 10
int queue[N + 1];
int head, tail;
int is_empty()
{
return (head == tail);
}
int is_full()
{
//queue에서 한 공간만 남았을 때를 꽉찼다고 하는데 이는 배열이 실제로 꽉차게 되면 head와 tail이 같아져 빈 queue와 구분할 방법이 없기 때문이다.
//modulo 대신에 tail == N인 경우에 1로 되도록 하는 ternary operator를 사용하였다.
//head == tail + 1
return (head == ((tail == N) ? 1: (tail + 1)));
}
int q_size()
{
int count = 0;
int temp = head;
while (temp != tail) {
count++;
temp = (temp == N) ? 1 : (temp + 1); //circular 구조를 고려
}
return count;
}
void enqueue(int item)
{
if (is_full()) {
printf("queue overflow\n");
exit(1);
}
queue[tail] = item;
tail = (tail == N) ? 1 : (tail + 1); //circular 고려한 tail += 1
}
int dequeue()
{
int item;
if (is_empty()) {
printf("queue underflow\n");
exit(1);
}
item = queue[head];
head = (head == N) ? 1 : (head + 1); //head 노드를 이제 그 다음 노드로 바꿔야 한다.
return item;
}큐가 꽉 찼는지 확인하는 함수에서 잘 보면 한 공간만 남았을 때를 꽉찼다고 하는데, 이는 배열이 실제로 꽉차게 만들면 head와 tail의 index가 같아져 빈 queue의 경우와 구분할 방법이 없어지기 때문입니다.
또한 modulo 연산자(%)대신, tail == N인 경우에 tail 값이 다시 1이 되고 tail != N이면 tail 값을 1 증가 시키도록 하는 ternary operator(삼항 연산자)를 사용하였습니다.
head == tail + 1
백준 문제(요세푸스 문제)
1158번: 요세푸스 문제
첫째 줄에 N과 K가 빈 칸을 사이에 두고 순서대로 주어진다. (1 ≤ K ≤ N ≤ 5,000)
www.acmicpc.net
입력: 첫째 줄에 N과 K가 빈 칸을 사이에 두고 순서대로 주어진다.
C 풀이
#include <stdio.h>
#include <stdlib.h>
#define N 10
int queue[N + 1];
int head, tail;
int is_empty()
{
return (head == tail);
}
int is_full()
{
//queue에서 한 공간만 남았을 때를 꽉찼다고 하는데 이는 배열이 실제로 꽉차게 되면 head와 tail이 같아져 빈 queue와 구분할 방법이 없기 때문이다.
//modulo 대신에 tail == N인 경우에 1로 되도록 하는 ternary operator를 사용하였다.
//head == tail + 1
return (head == ((tail == N) ? 1: (tail + 1)));
}
int q_size()
{
int count = 0;
int temp = head;
while (temp != tail) {
count++;
temp = (temp == N) ? 1 : (temp + 1); //circular 구조를 고려
}
return count;
}
void enqueue(int item)
{
if (is_full()) {
printf("queue overflow\n");
exit(0);
}
queue[tail] = item;
tail = (tail == N) ? 1 : (tail + 1); //circular 고려한 tail += 1
}
int dequeue()
{
int item;
if (is_empty()) {
printf("queue underflow\n");
exit(0);
}
item = queue[head];
head = (head == N) ? 1 : (head + 1); //head 노드를 이제 그 다음 노드로 바꿔야 한다.
return item;
}
int main()
{
int M, K, item, i, j, index;
scanf("%d %d", &M, &K);
head = tail = 1;
for (i = 1; i<=M; i++)
enqueue(i);
index = 0;
printf("<");
while (q_size() > 1)
{
index += K - 1;
if (q_size() <= index)
index %= q_size();
if (q_size() > 1)
printf("%d, ",dequeue());
else
printf("%d",dequeue());
}
printf(">");
return 0;
}
파이썬 풀이
n, k = map(int, input().split())
jo = []
for i in range(1, n+1):
jo.append(i)
print('<', end='')
index = 0
while len(jo) > 0:
index += k - 1
if len(jo) <= index:
index %= len(jo)
if len(jo) > 1:
print(jo.pop(index), end=', ')
else:
print(jo.pop(index), end='')
print('>', end='')
'CS 지식 > 자료구조와 알고리즘(Python)' 카테고리의 다른 글
| [자료구조와 알고리즘 | 파이썬] Graphs - 그래프 자료구조(+약간의 python 개념) (1) | 2022.12.31 |
|---|---|
| [자료구조와 알고리즘 | 파이썬] Trees (트리 자료구조) (0) | 2022.12.31 |
| [Python] Abstract Data Types (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Linked List(연결 리스트) | Singly linked list(단일 연결 리스트)와 Doubly linked list(이중 연결 리스트) (0) | 2022.12.31 |
| [자료구조와 알고리즘 | 파이썬] Sorting (정렬) (0) | 2022.12.31 |
소중한 공감 감사합니다