[데이터 통신] 3. 물리계층 이해(Introduction to Pysical Layer)
2023.02.13- -
3.1 Data and Signals
Communication at Physical Layer

physical layer는 전송 매체를 통해서 router, switch or 단말들이 데이터를 destination으로 보내는 것을 담당하고 있기 때문에 매 전송매체마다 (유무선 상관없이) physical 전송로(빨간색 선)를 따라 데이터를 보내주는 것에 대해 배워볼 것이다.
Analog and Digital Data
- To be transmitted, data must be transformed to electromagnetic signals.
- 데이터를 전송하기 위해서 electromagnetic signal로 변환을 해서 보내야 한다.
- Data can be analog or digital.
- Analog data are continuous and take continuous values.
- Digital data have discrete state and take on discrete values
- Signals can be analog or digital.
- Analog signals can have an infinite number of values in a range
- Digital signals can have only a limited number of defined values.
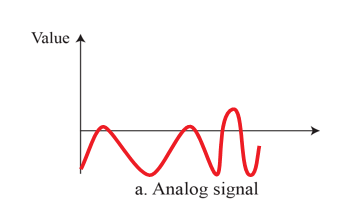
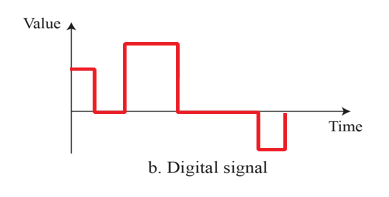
Periodic and Non-periodic Signals
- In data communication, we commonly use periodic analog signals and non-periodic digital signals.
- 특정 주기 내에 똑같은 form의 signal이 반복되는 형태
- 위의 두 그림은 periodic 신호이고 아래 두 그림은 non-periodic 신호이다.

3.2 Periodic Analog Signals
- Periodic analog signals can be classified as simple or composite.
- A simple periodic analog signal, a sine wave, cannot be decomposed into simpler signals.
- 이보더 더 간단한 signal로 분해될 수 없는 signal
- ex) sine wave
- A composite periodic analog signal is composed of multiple sine waves
- A simple periodic analog signal, a sine wave, cannot be decomposed into simpler signals.
- Sine wave is described by
- Peak Amplitude
- Period (1/frequency)
- Phase
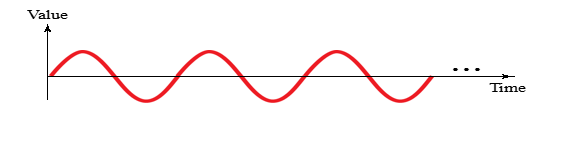
Peak Amplitude
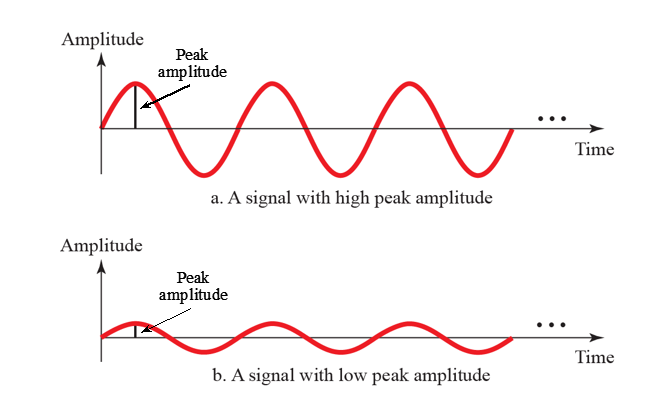
high peak amplitude vs. low peak amplitude
Period and Frequency(주기와 주파수)
- Frequency and period are the inverse of each other
- frequency와 period는 서로 역수 관계에 있다.
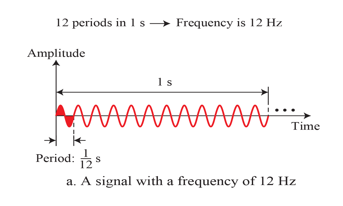
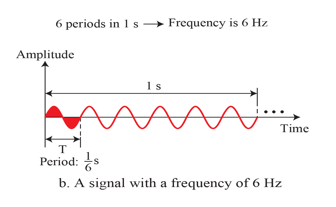
Units of Period and Frequency

<table 3.1>
Example 3.4, 3.5
- Express a period of 100 ms in microseconds, and express the corresponding frequency in kilohertz
From Table 3.1 we find equivalent of 1 ms. We make the following substitutions:
- 100 ms = 100 x 10-3 s = 100 x 10-3 x 106 ms = 105 us
Now we use the inverse relationship to find the frequency, changing hertz to kilohertz
- 100 ms = 100 x 10-3 s = 10-1 s
- f = 1/10-1Hz = 10 x 10-3 KHz = 10-2 KHz
More About Frequency
- Another way to look frequency
- Frequency is the rate of change with respect to time
- 시간에 대한 변화율
- Change in a short span of time means high frequency(span = 기간)
- 짧은 시간의 기간동안에 변화가 일어나면 고주파(high frequency이다.)
- Change over a long span of time means low frequency
- Frequency is the rate of change with respect to time
- Two extremes
- No change at all => zero frequency
- Instantaneous changes => infinite frequency
Phase
- Phase describes the position of the waveform relative to time zero.

Example 3.6
- A sine wave is offset 1/6 cycle with respect to time 0.
What is its phase in degrees and radians?
We know that one complete cycle is 360 degrees.
Therefore, 1/6 cycle is (1/6) 360 = 60 degrees = 60 x 2 x pi x 360 rad = 1.046 rad
Wavelength
- Another characteristic of a signal traveling through a transmission medium
- Binds the period or the frequency of a simple sine wave to the
propagation speedof the medium - Wavelength = propagation speed x period
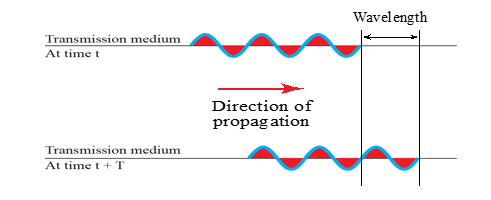
- = propagation speed / frequency
Time and Frequency Domains
- A complete sine wave in the time domain can be represented by one single spike in the frequency domain
- time-domain
- frequency-domain
Example 3.7
- Time domain and frequency domain of three sine waves with frequencies 0, 8, 16
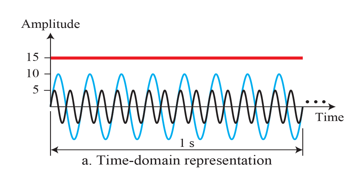

Composite Signals
- A single-frequency sine wave is not useful in data communications.
- So, we need to send a composite signal which is a signal made of many simple sine waves.
- 수많은 simple sine wave들로 만들어진 composite signal을 보내야 함.
- When we change one or more characteristics of a single-frequency signal, it becomes a composite signal made of many frequencies
- According to Fourier analysis, any composite signal is a combination of simple sine waves with different frequencies, phases, and amplitudes
- If the composite signal is periodic, the decomposition gives a series of signals with discrete frequencies; if the composite signal is non-periodic, the decomposition gives a combination of sine waves with continuous frequencies.
- 즉 composite signal이 non-periodic하면 연속적인(무수히 많은) frequency들의 결합으로 signal이 만들어질 수 있다.
- 반대로 periodic하면 discrete한(특정 값을 가지는) frequency들의 결합으로 signal이 표현 될 수 있다.
Composite Periodic Signal

digital signal에 가까운 composite signal이 있을 때 이 signal은 세 가지의 discrete한 주파수 성분을 갖는 신호들의
합
으로 표현된다.
이 중 빨간 선으로 표시된 신호가 first harmony, 즉 가장 낮은 주파수이다.
- first harmony는 (나중에 배우는 표현) bit rate의 절반이다.
Composite Non-periodic Signal

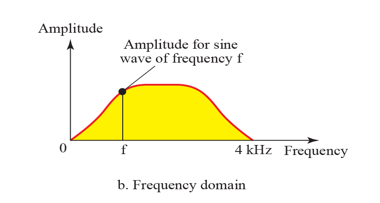
non-periodic composite signal을 주파수 domain에서 봤을 때 continuous 한 signal을 보인다.
Bandwidth
- The bandwidth of a composite signal is the difference between the highest and the lowest frequencies contained in that signal
- high frequency와 low frequency 간의 차이


- 두 그림 모두 low frequency는 1000Hz이고 high frequency는 5000Hz이므로 두 그래프의 bandwidth는 4000Hz이다.
- 왼쪽 그림은 discrete frequency 값들을 가지므로 composite periodic signal 이고 오른쪽 그림은 continuous frequency 값들을 가지므로 composite non-periodic signal이다.
Example 3.11
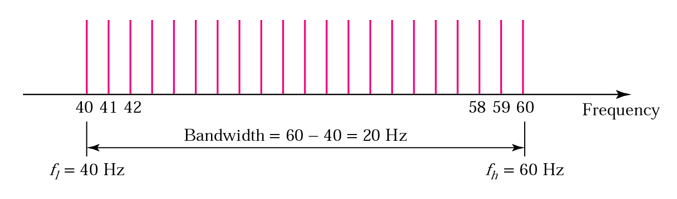
- A signal has a bandwidth of 20 Hz. The highest frequency is 60Hz. What is the lowest frequency? Draw the spectrum if the signal contains all integral frequencies of the same amplitude
- B = fh - fb
- 20 = 60 - fb
- fl = 60 - 20 = 40 Hz
3.3 Digital Signals


8 bits per second 16 bits per second
- discrete한 value를 전달한다.
- 왼쪽은 2-level, 8 bps
- 오른쪽은 4-level, 16 bps
Bit Rate and Bit Length
- Most digital signals are non-periodic, and thus period and frequency are not appropriate characteristics. Bit rate (instead of frequency) is used to describe digital signals
- Bit rate: the number of bits sent in 1s, expressed in bits per second (bps)
- 1초 안에 보낼 수 있는 bit의 숫자
- Bit Length: the distance one bit occupies on the transmission medium
Bit length = propagation speed x bit duration
Example 3.18
- Assume we need to download text documents at the rate of 100 pages per second. What is the required bit rate of the channel?
Solution)
- A page is an average of 24 lines with 80 characters in each line. If we assume that one character requires 8 bits, the bit rate is
- 100 x 24 x 80 x 8 =1,536,000 bps = 1.536 Mbps
Digital Signal as a Composite Analog Signal
Digital signal도 analog signal과 유사하다.

- non-periodic digital signal -> continuous frequency signal
- periodic digital signal -> discrete frequency signal
- digital signal은 다수의 analog signal의 결합으로 구성된다.
Transmission of Digital Signals
- A digital signal is a composite analog signal with an infinite bandwidth
- 어떠한 주파수 대역이든지 전달하기 위해 infinite한 bandwidth를 가지는 signal이 필요하다.
- continuous frequency signal은 infinite bandwidth를 가진다.
- Baseband transmission: Sending a digital signal without changing into an analog signal
- digital signal을 analog signal로 변조(modulation)하지 않고 그대로 보내는 것(sending)
- Baseband transmission requires a low-pass channel
- 저주파부터 시작하여 많은 주파수를 통과시켜야한 original signal을 유지할 수 있다.

Bandwidths of Two Low-Pass Channels
앞서 말한 것처럼 signal을 digital-to-analog로 변조 시키지 않고 보내기 위해선 저주파 bandwidth를 가져야 한다.
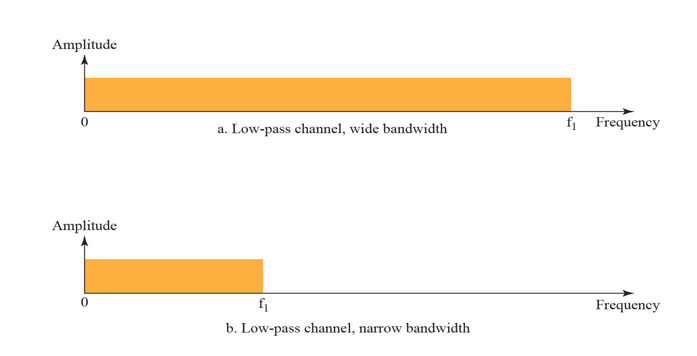
주파수가 통과하는 대역
- 대역이 넓을 수록 original signal를 많이 통과시킴으로써 원형을 대부분을 보장할 수 있지만, 반대의 경우 원형에 손상이 입은 결과가 나타난다.
Low-Pass Channel with Wide Bandwidth
- Baseband transmission of a digital signal that preserves the shape of the digital signal is possible only if we have a low-pass channel with infinite or very wide bandwidth
- Baseband transmission: digital 신호를 아날로그 신호로 변조하지 않고 그대로 digital 신호로 보내는 것
- Baseband transmission using a dedicated medium
- 전송을 하기 위해 channel에 들어가는데 channel은 특정 bandwidth를 갖는다.
- bandwidth 밖의 input signal들은 버려지게 된다.

- 세상에 어떠한 channel도 무한대의 주파수 대역(bandwidth)를 갖고있지 않기 때문에 특정 signal을 보낼 때 완전히 100% 복원하는 것은 불가능하지만
- digital 신호는 0과 1밖에 없기 때문에 넓은 bandwidth를 가짐으로써 이 둘(0,1)의 구분을 망치는 정도의 간섭이 없다면 꽤 정확하게 복원이 가능하다.
Low-Pass Channel with Limited Bandwidth
- Rough approximation of a digital signal using the first harmonic for worst case
- N: bit rate
- bit rate의 절반이 first harmoy이다.

first harmony만을 가지고 이용하여, 즉 N/2 , bit rate의 절반 정도의 신호 성분만을 갖는다고 가정하면 어떠한 일이 일어날까?
Low-Pass Channel with Limited Bandwidth
- Rough approximation
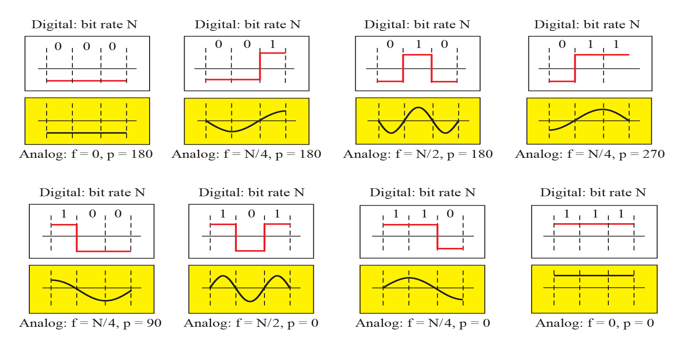
가장 높은 주파수를 갖는 경우는 f=N/2일 때이고 기껏해 봐야 해당 그림만큼밖에 근사가 가능하다.
- Better approximation with first three harmonics
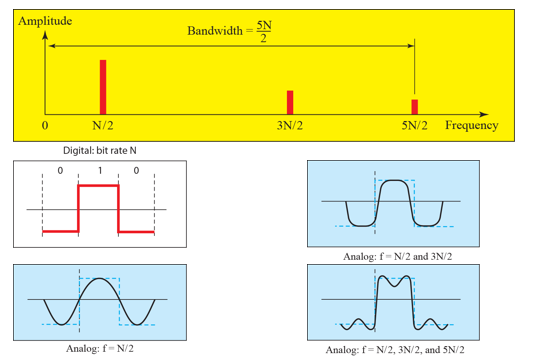
만약 통과시킬 bandwidth가 5N/2 이라고 가정해 보자.
그러면 N/2의 신호만 보내게 될 때와 비교했을 때 3N/2와 5N/2를 포함 시킬 수록 더욱 original 신호에 가까워 지는 것을 볼 수 있다.
물론 더 높은 harmony의 주파수가 포함이 되도록 bandwidth가 커지면 더 discrete signal과 가까운 신호가 되는 것이다.
즉, 낮은 주파수 밖에 사용할 수 없다면 신호 자체가 왜곡이 될 수 밖에 없다. 왜냐면 original 신호를 구성했던 많은 높은 주파수 성분들이 low pass filter를 통과시키면서 다 날아가게 되고 bandwidth 안의 성분만 전달이 되기 때문에 신호가 왜곡되는 현상이 발생할 수밖에 없다.
Bandwidth Requirement
- In baseband transmission, the required bandwidth is proportional to the bit rate; if we need to send bits faster, we need more bandwidth

bit rate과 비례하여 요구되는 bandwidth의 크기가 증가하며 많은 harmonic을 포함시기 위해서 그 만큼 높은 bandwidth가 요구됨을 알 수 있다.
Broadband Transmission (Using Modulation)
- Modulation(변조) allows us to use a bandpass channel
- If the available channel is a bandpass channel, we cannot send the digital signal directly to the channel
- we need to convert the digital signal to and an analog signal before transmission.
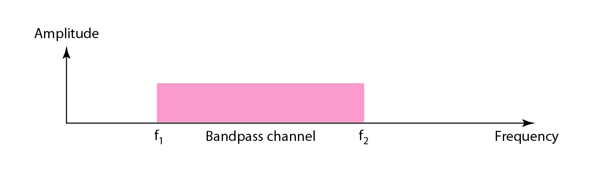
- modulation: bandpass 특정 주파수 대역으로 신호를 옮기는 것
- digital 신호를 analog 신호로 변환한 다음에 전송한다.
- 예를 들어, 어떠한 데이터를 케이블 혹은 FM의 한 채널로 보내겠다고 하면 해당 데이터를 보내고 싶은 특정 channel의 주파수 대역으로 analog로 modulation 시킨다음에 보내야 하는 것이다.
Modulation of Digital Signal for Transmission on a Bandpass Channel

- Input digital signal을 Digital to analog converting 과정을 진행한다.
- f1~f2 bandpass 주파수 대역으로 modulation을 하고
- 우리가 원하는 channel을 통과하게 되며,
- 통과된 신호는 다시 Analog to digital converting 과정을 진행하면 original digital 신호(output signal)를 복원하게 된다.
위 과정을 broadband transmission이라고 한다.
3. 4 Transmission Impairment
데이터는 전송하는 과정에서 보통 장애를 입기 마련이다.
이와 같이 original 신호가 목적지에 도착했을 때 원래 신호와 모양이 달라지는 것을 Impairment라고 하는데 아래와 같은 중요 3가지의 원인이 존재한다.

- Attenuation: 감쇠(신호 level이 떨어진다.)
- Distortion: 왜곡(뒤틀림)
- Noise: 잡음
Attenuation(감쇠)
- Loss of energy to overcome the resistance of the medium: heat
- 충돌 등에 의해 에너지가 소비 됨

- 충돌 등에 의해 에너지가 소비 됨
떨어진 신호 level을 높여주기 위해 Amplifier로 복원시키는 것이 가능하다.
Decibel
- Example 3.26:
- Suppose a signal travels through a transmission medium and its power is reduced to one-half. This means that P2 = (1/2)P1. In this case, the attenuation (loss of power) can be calculated as

- Example 3.28
amplifier를 통해 overall 1db의 gain을 얻어냈다.
Distortion(왜곡)
- 감쇠보다 더 까다로움
- The signal changes its form or shape
- Each signal component in a composite signal has
its own propagation speed
- Differences in delay may cause a difference in phase
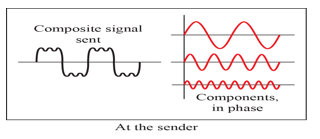

- composite signal은 저주파부터 고주파까지 다양한 주파수 성분들이 존재하는데 각각의 다른 주파수를 갖는 성분들이 전달되는 과정에서 각자가 다 다른 propagation speed를 가질 것이다. 그렇기 때문에 도착했을 때 신호가 제각기 도착하여 뒤틀리는 현상이 발생한 것이다.
- 그래서 이를 증폭한다고 해결할 수있는 문제가 아니기 때문에 까다로운 것이다.
Noise
- Several types of noises, such as thermal noise, induced noise, crosstalk, and impulse noise, may corrupt the signal

Noise와 같은 외부 요인이 Transmission medium에 들어옴으로써 장애를 발생시킴.
Signal-to-Noise Ratio (SNR)
- To find the theoretical bit rate limit
- 이에 따라 이론적으로 보낼 수 있는 bit rate가 결정됨
- SNR = average signal power/average noise power
- SNRdB = 10 log10SNR
- Example 3.31: The power of a signal is 10 mW and the power of the noise is 1uW
- What are the values of SNR and SNRdB
Solution:

signal power가 외부로부터 들어오는 noise power의 10,000배가 된다.
Two Cases of SNRs


SNR이 높을 수 록 더 높은 bit rate에서 전송이 가능하다.
3.5 Data Rate Limits
- Data rate depends on three factors:
- Bandwidth available
- 넓을수록 빨리 보낼 수 있다.
- Level of the signals we use
- level이 많을 수록 그 만큼 보낼 수 있는 bit 수가 늘아나기 때문에 빨리 보낼 수 있다.
- Quality of the channel (the noise level)
- Bandwidth available
- Noiseless channel: Nyquist Bit Rate
- 노이즈가 없다고 가정
- Bit rate = 2 * Bandwidth * log2L
- Increasing the levels may cause the reliability of the system
- 똑같은 bandwidth를 가진다고 할 때 L값을 높여서 Bit rate를 높이는 것이 좋지만 무작정 level을 올린다고 좋은 것이 아님. (reliability의 오류 가능성이 높아짐)
- Noisy channel: Shannon Capacity
- Capacity = Bandwidth * log2(1 + SNR)
Nyquist Bite Rate: Examples
level을 늘려 bit rate을 높이는 경우를 알아보자.
- Consider a noiseless channel with a bandwidth of 3000 Hz transmitting a signal with two signal levels. The maximum bit rate can be calculated as
- Bit Rate = 2 X 3000 X log22 = 6000 bps
- Consider the same noiseless channel, transmitting a signal with four signal levels (for each level, we send two bits). The maximum bit rate can be calculated as:
- Bit Rate = 2 X 3000 X log24 = 12,000 bps
이를 통해 같은 bandwidth에서 신호 level 갯수를 늘리는 것으로 두 배의 bps를 얻어낼 수 있음을 알 수 있다.
Shannon Capacity: Examples
- Consider an extremely noisy channel in which the value of the signal-to-noise ratio is almost zero. In other words, the noise is so strong that the signal is faint. For this channel the capacity is calculated as
- C = B log2 (1 + SNR) = B log2 *(1 + 0) = B log2 (1) = B X 0 = 0
- We can calculate the theoretical highest bit rate of a regular telephone line. A telephone line normally has a bandwidth of 3000 Hz (300 Hz to 3300 Hz). The signal-to-noise ratio is usually 3162. For this channel the capacity is calculated as
- C = B log2(1 + SNR) = 3000 log2(1 + 3162) = 3000 log2(3163)
- C = 3000 X 11.62 = 34,860 bps
Using Both Limits
- The Shannon capacity gives us the upper limit; the Nyquist formula tells us how many signal levels we need.
- Example: We have a channel with a 1 MHz bandwidth. The SNR for this channel is 63; what is the appropriate bit rate and signal level?
First, we use the Shannon formula to find our upper limit
C = B log2(1 + SNR) = 106 log2(1 + 63)
= 106 log2 (64) = 6Mbps
Then we use the Nyquist formula to find the number of signal levels
4 Mbps = 2 x 1 MHz X log2L → L = 4
단지 upper limit이 6Mbps라고 signal level을 조절하여 6Mbps로 똑같이 맞춰버리지 말고 그보다 더 낮은 4Mbps로 맞춰야 한다.(upper limit은 말 그대로 upper limit이므로 딱 그 값으로 되면 적절하지 않음)
3.6 Performance를 결정하는 요소
- Bandwidth (in two contexts)
- Bandwidth in hertz, refers to the range of frequencies in a composite signal or the range of frequencies that a channel can pass.
- Bandwidth in bits per second(bps), refers to the speed of bit transmission in a channel or link.
- Throughput
- Measurement of how fast we can actually send data through a network
- 실질적인 데이터의 나가는 속도
- Latency(Delay)
- Define how long it takes for an entire message to completely arrive at the destination from the time the first bit is sent out from the source(delay)
- Latency =
propagation time(전송매체를 통해 전달되는 시간) + transmission time(전송시간) + queuing time(대기 시간) + processing delay- Propagation time = Distance/Propagation speed (줄이기 어려움)
- Transmission time = Message size/Bandwidth (bandwidth를 넓을 것을 쓰면 줄일 수 있다.)
- Jitter
- delay의 variation(편차)
- 여러 개의 packet 하나하나가 겪게 될 delay적인 요소가 다 다르기 때문에 일정한 간격으로 나갔다고 해도 일정한 간격으로 도착하지 않는데 이러한 delay를 말한다.
Bandwidth-Delay Product
- The bandwidth-delay product(곱) defines the number of bits that can fill the link
- Filling the link bits for case 1

- 5 bits mean 이 링크 전체를 채우는 숫자
- 위 예시는 1초에 1bit씩 날아가고 sender 부터 reciever까지 가는데 걸리는 delay가 5s인 상황이다.
- 이 때 5초가 지나면 1bps x 5s = 5 bits 가 link 전체를 채우게 된다는 것을 의미하는 지표이다.
- Filling the link bits for case 2


- link를 채운 전체 bit 수 = 25 bits
- 이 bandwidth delay product을 파이프라인에 비유하면
- 굵기 : bandwidth
- 길이: delay
- 따라서 굵기와 길이를 곱하면 이 파이프 라인을 가득 채우는 양, 즉 비트 수를 표현한 값이다.
- 무슨 의미가 있는가?
- 현재는 정보 및 네트워크의 발전에 따라 전송하는 단위가 몇 메가 bps를 넘어가면서 요구되는 bandwidth는 자꾸만 넓어지지만 sender-receiver 사이의 delay는 여전히 줄이기가 어렵다.
- 비유하자면 파이프 전체를 채우는 데이터의 양이 늘어나는 것이다.
- 즉, 다시말해서 파이프의 굵기는 굉장히 굵어지는데 반해 길이는 줄어들지 않아서,
- 첫 번째로 보낸 정보가 receiver까지 잘 전달이 되고 이에 대해 잘 받았다는 응답이 보통은 오는데 이 응답을 받기 전까지 네트워크에 내놓아야 할 bandwidth delay product 데이터가 너무 많게 된다.
- 예를 들면, 위 예제에서 25bits로 나가고 이것을 잘 받은 다음에 receiver가 응답을 준다면 첫 번째 first 5 bits를 보낸 다음에 이것을 잘 받았다는 응답을 받는 데까지는 bandwidth delay product의 두 배(오고 가는 시간이 있기 때문에) 즉, 엄청나게 많은 데이터가 첫번째 데이터가 잘 받았다는 확신이 없는 상태에서도 network에 쏟아져 나오게 되는 것이다.
- 현재는 정보 및 네트워크의 발전에 따라 전송하는 단위가 몇 메가 bps를 넘어가면서 요구되는 bandwidth는 자꾸만 넓어지지만 sender-receiver 사이의 delay는 여전히 줄이기가 어렵다.
'CS 지식 > 네트워크' 카테고리의 다른 글
| [데이터 통신] 6. Bandwidth Utilization Multiplexing & Specturm Spreading (0) | 2023.02.13 |
|---|---|
| [데이터 통신] 5. 아날로그 전송(Analog Transmission) (0) | 2023.02.13 |
| [데이터 통신] 4. 디지털 전송(Digital Transmission) (0) | 2023.02.13 |
| [데이터 통신] 2. 네트워크 모델(Network Models) (0) | 2023.02.13 |
| [데이터 통신] 1. 데이터 통신 및 네트워크를 시작하며 (0) | 2023.02.13 |
소중한 공감 감사합니다


